题目内容
【题目】已知在□ABCD中,AEBC于E,DF平分ADC 交线段AE于F.
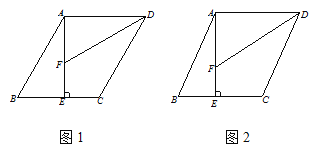
(1)如图1,若AE=AD,ADC=60, 请直接写出线段CD与AF+BE之间所满足的等量关系;
(2)如图2, 若AE=AD,你在(1)中得到的结论是否仍然成立, 若成立,对你的结论加以证明, 若不成立, 请说明理由;
【答案】(1)CD=AF+BE.(2)(1)中的结论仍然成立.证明见解析.
【解析】试题分析:(1)、利用截长补短法可以得出线段之间的关系;(2)、延长EA到G,使得AG=BE,连结DG,根据平行四边形的性质得出△ABE和△DAG全等,从而得出DG=AB,根据角度之间的关系得出DG=GF,即CD=GF=AF+AG=AF+BE得出答案.
试题解析:(1)、CD=AF+BE.
(2)、解:(1)中的结论仍然成立.
证明:延长EA到G,使得AG=BE,连结DG,
∵ 四边形ABCD是平行四边形, ∴ AB=CD,AB∥CD,AD=BC,
∵ AE⊥BC于点E, ∴ ∠AEB=∠AEC=90, ∴∠AEB=∠DAG=90, ∴ ∠DAG=90,
∵ AE=AD, ∴ △ABE≌△DAG, ∴∠1=∠2, DG=AB, ∴∠GFD=90-∠3,
∵ DF平分∠ADC, ∴∠3=∠4,
∴∠GDF=∠2+∠3=∠1+∠4=180-∠FAD-∠3=90-∠3, ∴∠GDF=∠GFD,∴ DG=GF.
∴ CD=GF=AF+AG= AF + BE, 即 CD = AF +BE.

练习册系列答案
相关题目