��Ŀ����
�Ķ����ϣ���ѧ�Ҹ�˹����ѧʱ�����о�������һ�����⣬1+2+3+��+10=��
�����о�����������һ���Խ�����1+2+3+��+n=![]() n��n+1��������nΪ�������������������о�һ�����Ƶ����⣺1��2+2��3+��+ n��n+1��=��
n��n+1��������nΪ�������������������о�һ�����Ƶ����⣺1��2+2��3+��+ n��n+1��=��
�۲�������������ĵ�ʽ��
1��2=![]() ��1��2��3-0��1��2��
��1��2��3-0��1��2��
2��3=![]() ��2��3��4-1��2��3��
��2��3��4-1��2��3��
3��4=![]() ��3��4��5-2��3��4��
��3��4��5-2��3��4��
����������ʽ��������ӣ����Եõ�1��2+2��3+3��4=![]() ��3��4��5=20.
��3��4��5=20.
������β��ϣ�������㣺
��1��1��2+2��3+��+100��101����ֻ��д���������2�֣�
��2��1��2+2��3+��+ n��n+1����(д���������) ��5�֣�
��3��1��2��3+2��3��4+��+ n��n+1����n+2������ֻ��д���������3�֣�
��1�� 343400��
��2�� ![]() n(n+1)(n+2)
n(n+1)(n+2)
(3) ![]() n(n+1)(n+2)(n+3)
n(n+1)(n+2)(n+3)

��ϰ��ϵ�д�
�����Ŀ
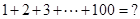
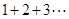
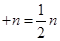
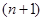 ������
������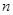 ����������
����������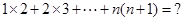
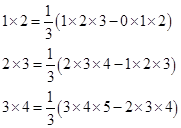
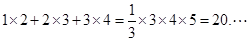
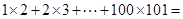 ��������������___________________��;������
��������������___________________��;������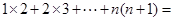 ��������������______________________ ��;����������������
��������������______________________ ��;����������������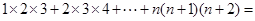 ��������������___________��.��������������
��������������___________��.��������������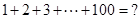
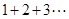
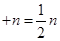
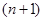 ������
������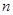 ����������
����������
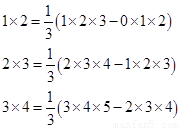
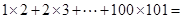 ��������������___________________��;������
��������������___________________��;������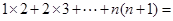 ��������������______________________ ��;����������������
��������������______________________ ��;����������������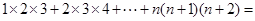 ��������������___________��.��������������
��������������___________��.��������������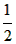 n��n+1��������nΪ�������������������о�һ�����Ƶ����⣺1��2+2��3+��+n��n+1��=��
n��n+1��������nΪ�������������������о�һ�����Ƶ����⣺1��2+2��3+��+n��n+1��=��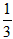 ��1��2��3-0��1��2��
��1��2��3-0��1��2��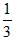 ��3��4��5-2��3��4��
��3��4��5-2��3��4��