题目内容
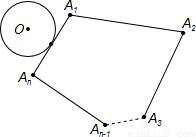
如图，⊙O沿凸多边形A1A2A3…An-1An的外侧（圆与边相切）作无滑动的滚动．假设⊙O的周长是凸多边形A1A2A3…An-1An的周长的一半，那么当⊙O回到出发点时，它自身滚动的圈数为
- A.1
- B.2
- C.3
- D.4
C
分析：因为⊙O的周长是凸多边形A1A2A3…An-1An的周长的一半，所以⊙O在边上滚动正好两周，另外凸多边形的外角和为360°，所以⊙O在角处共滚动一周，可以求出⊙O滚动的圈数．
解答：由于凸多边形周长是圆周长的2倍，另外凸多边形的外角和是360°，
所以⊙O回到出发点时共滚动2+1=3圈．
故选C．
点评：本题考查的是对圆的认识，根据⊙O的周长是凸多边形A1A2A3…An-1An的周长的一半，可以知道圆在边上滚动两周，然后由多边形外角和是360°，可以知道圆在角处滚动一周．因此可以求出滚动的总圈数．
分析：因为⊙O的周长是凸多边形A1A2A3…An-1An的周长的一半，所以⊙O在边上滚动正好两周，另外凸多边形的外角和为360°，所以⊙O在角处共滚动一周，可以求出⊙O滚动的圈数．
解答：由于凸多边形周长是圆周长的2倍，另外凸多边形的外角和是360°，
所以⊙O回到出发点时共滚动2+1=3圈．
故选C．
点评：本题考查的是对圆的认识，根据⊙O的周长是凸多边形A1A2A3…An-1An的周长的一半，可以知道圆在边上滚动两周，然后由多边形外角和是360°，可以知道圆在角处滚动一周．因此可以求出滚动的总圈数．
练习册系列答案
相关题目
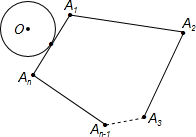
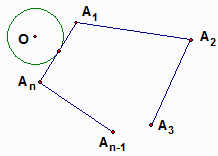6、如图，⊙O沿凸多边形A1A2A3…An-1An的外侧（圆与边相切）作无滑动的滚动．假设⊙O的周长是凸多边形A1A2A3…An-1An的周长的一半，那么当⊙O回到出发点时，它自身滚动的圈数为（ ）
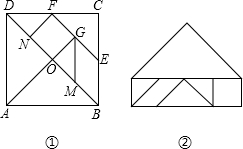对正方形ABCD分划如图①，其中E、F分别是BC、CD的中点，M、N、G分别是OB、OD、EF的中点，沿分划线可以剪出一副由七块部件组成的“七巧板”．
对正方形ABCD分划如图①，其中E、F分别是BC、CD的中点，M、N、G分别是OB、OD、EF的中点，沿分划线可以剪出一副由七块部件组成的“七巧板”．
