题目内容
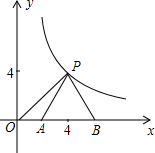 (2013•柳州)如图,点P(a,a)是反比例函数y=
(2013•柳州)如图,点P(a,a)是反比例函数y=| 16 |
| x |
分析:如图,根据反比例函数系数k的几何意义求得点P的坐标,则易求PD=4.然后通过等边三角形的性质易求线段AD=
,所以S△POA=
OA•PD=
×
×4=
.
4
| ||
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
12-4
| ||
| 3 |
24-8
| ||
| 3 |
解答: 解:如图,∵点P(a,a)是反比例函数y=
解:如图,∵点P(a,a)是反比例函数y=
在第一象限内的图象上的一个点,
∴16=a2,且a>0,
解得,a=4,
∴PD=4.
∵△PAB是等边三角形,
∴AD=
.
∴OA=4-AD=
,
∴S△POA=
OA•PD=
×
×4=
.
故选D.
 解:如图,∵点P(a,a)是反比例函数y=
解:如图,∵点P(a,a)是反比例函数y=| 16 |
| x |
∴16=a2,且a>0,
解得,a=4,
∴PD=4.
∵△PAB是等边三角形,
∴AD=
4
| ||
| 3 |
∴OA=4-AD=
12-4
| ||
| 3 |
∴S△POA=
| 1 |
| 2 |
| 1 |
| 2 |
12-4
| ||
| 3 |
24-8
| ||
| 3 |
故选D.
点评:本题考查了反比例函数系数k的几何意义,等边三角形的性质.等边三角形具有等腰三角形“三合一”的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2013•柳州)如图是经过轴对称变换后所得的图形,与原图形相比( )
(2013•柳州)如图是经过轴对称变换后所得的图形,与原图形相比( )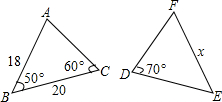 (2013•柳州)如图,△ABC≌△DEF,请根据图中提供的信息,写出x=
(2013•柳州)如图,△ABC≌△DEF,请根据图中提供的信息,写出x=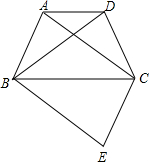 (2013•柳州)如图,四边形ABCD为等腰梯形,AD∥BC,连结AC、BD.在平面内将△DBC沿BC翻折得到△EBC.
(2013•柳州)如图,四边形ABCD为等腰梯形,AD∥BC,连结AC、BD.在平面内将△DBC沿BC翻折得到△EBC.  (2013•柳州)如图,⊙O的直径AB=6,AD、BC是⊙O的两条切线,AD=2,BC=
(2013•柳州)如图,⊙O的直径AB=6,AD、BC是⊙O的两条切线,AD=2,BC=