Question

【题目】如图，在△ABC中，AD是BC边上的高，tanC= ，AC=3 ，AB=4，求△ABC的周长．

Answer 1

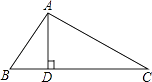
【答案】解：在Rt△ADC中，tanC= = ， 设AD=k，CD=2k，
AC= = k，
∵AC=3 ，
∴ k=3 ，解得k=3，
∴AD=3，CD=6，
在Rt△ABD中，
BD= = = ，
∴△ABC的周长=AB+AC+BD+CD=4+3 + +6=10+3 +
【解析】在Rt△ADC中，根据正切的定义得到tanC= = ，则可设AD=k，CD=2k，接着利用勾股定理得到AC= k，则 k=3 ，解得k=3，所以AD=3，CD=6，然后在Rt△ABD中，利用勾股定理计算出BD= ，再根据三角形的周长的定义求解．
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2，以及对解直角三角形的理解，了解解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)．