题目内容
(2001•湖州)如图,已知两圆相交于CD两点,AB为两圆的外公切线,A、B为切点,CD的延长线交AB于M,若MD=3,CD=9,则AB的长等于 .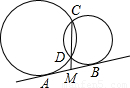
【答案】分析:根据切割线定理得AM2=MD•MC=36,BM2=MD•MC,从而可求得AM=BM=6,即得到了AB的长.
解答:解:∵AM2=MD•MC=36,BM2=MD•MC,MD=3,CD=9;
∴AM=BM=6,
∴AB=12.
点评:此题主要是运用切割线定理进行计算.
解答:解:∵AM2=MD•MC=36,BM2=MD•MC,MD=3,CD=9;
∴AM=BM=6,
∴AB=12.
点评:此题主要是运用切割线定理进行计算.

练习册系列答案
相关题目