题目内容
【题目】如图,已知△ABC是边长为2的等边三角形,点D在边BC上,将△ABD沿着直线AD翻折,点B落在点B1处,如果B1D⊥AC,那么BD= . 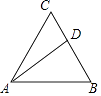
【答案】2 ![]() ﹣2
﹣2
【解析】解:作DE⊥AB于E, 由折叠的性质可知,∠B′=∠B=60°,
∵B1D⊥AC,
∴∠B′AC=30°,
∴∠B′AC=90°,
由折叠的性质可知,∠B′AD=∠BAD=45°,
在Rt△DEB中,DE=BD×sin∠B= ![]() BD,BE=
BD,BE= ![]() BD,
BD,
∵∠BAD=45°,DE⊥AB,
∴AE=DE= ![]() BD,
BD,
则 ![]() BD+
BD+ ![]() BD=2,
BD=2,
解得,BD=2 ![]() ﹣2,
﹣2,
故答案为:2 ![]() ﹣2.
﹣2.
作DE⊥AB于E,根据折叠的性质、三角形内角和定理求出∠B′AC=30°,求出∠BAD=45°,利用锐角三角函数的概念计算即可.

练习册系列答案
相关题目