题目内容
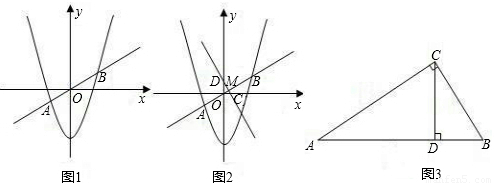
如图M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=45°,且DM交AC于F,ME交BC于G,连接FG,若AB= ,AF=3,则BG= ,FG= .
,AF=3,则BG= ,FG= .
【答案】分析:根据已知条件,∠DME=∠A=∠B=45度,结合图形上的公共角∠E,即可推出AMF∽△BGM,再根据相似三角形的性质,推出BG的长度,依据锐角三角函数推出AC的长度,即可求出CG、CF的长度,继而推出FG的长度.
解答:解:∵∠AFM=∠DME+∠E(外角定理),
∠DME=∠A=∠B(已知),
∴∠AFM=∠DME+∠E=∠A+∠E=∠BMG,∠A=∠B,
∴△AMF∽△BGM,
∵∠DME=∠A=∠B=45°
∴AC=BC,∠ACB=90°,
∴AC⊥BC,
∵M为AB的中点,
∴AM=BM=2 ,
,
∵△AMF∽△BGM,
∴ ,
,
∴BG= =
= ,
,
AC=BC=4 cos45°=4,
cos45°=4,
∴CG=4- =
= ,CF=4-3=1,
,CF=4-3=1,
在Rt△FCG中,由勾股定理得:
FG= =
= =
= .
.
故答案为: ,
, .
.
点评:本题主要考查相似三角形的判定和性质、解直角三角形、等腰三角形的性质,解题的关键找到相似的三角形,根据其性质求出BG、FG的长度.
解答:解:∵∠AFM=∠DME+∠E(外角定理),
∠DME=∠A=∠B(已知),
∴∠AFM=∠DME+∠E=∠A+∠E=∠BMG,∠A=∠B,
∴△AMF∽△BGM,
∵∠DME=∠A=∠B=45°
∴AC=BC,∠ACB=90°,
∴AC⊥BC,
∵M为AB的中点,
∴AM=BM=2
 ,
,∵△AMF∽△BGM,
∴
 ,
,∴BG=
 =
= ,
,AC=BC=4
 cos45°=4,
cos45°=4,∴CG=4-
 =
= ,CF=4-3=1,
,CF=4-3=1,在Rt△FCG中,由勾股定理得:
FG=
 =
= =
= .
.故答案为:
 ,
, .
.点评:本题主要考查相似三角形的判定和性质、解直角三角形、等腰三角形的性质,解题的关键找到相似的三角形,根据其性质求出BG、FG的长度.

练习册系列答案
相关题目

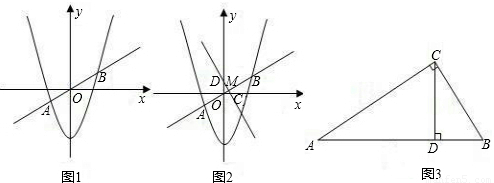
 与直线
与直线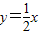 相交于A,B两点.
相交于A,B两点.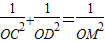 是否成立;
是否成立;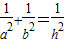 .
.
 与直线
与直线 相交于A,B两点.
相交于A,B两点. 是否成立;
是否成立; .
.
 与直线
与直线 相交于A,B两点.
相交于A,B两点. 是否成立;
是否成立; .
.
 与直线
与直线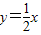 相交于A,B两点.
相交于A,B两点. 是否成立;
是否成立;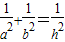 .
.