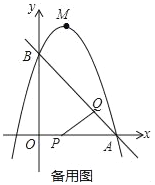
题目内容
【题目】已知![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,作
,作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() .
.
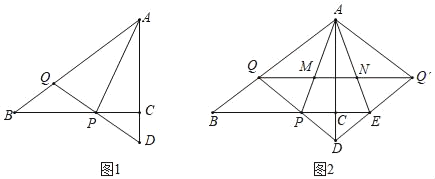
(感知)如图①,点![]() 、
、![]() 在
在![]() 同侧,且点
同侧,且点![]() 在
在![]() 右侧,在射线
右侧,在射线![]() 上截取
上截取![]() ,连接
,连接![]() ,可证
,可证![]() ,从而得出
,从而得出![]() ,
,![]() ,进而得出
,进而得出![]() 度.
度.
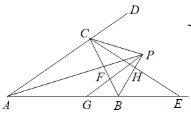
(探究)如图②,当点![]() 、
、![]() 在
在![]() 异侧时,(感知)得出的
异侧时,(感知)得出的![]() 的大小是否改变?若不改变,给出证明;若改变,请求出
的大小是否改变?若不改变,给出证明;若改变,请求出![]() 的大小.
的大小.
(应用)在直线![]() 绕点
绕点![]() 旋转的过程中,当
旋转的过程中,当![]() ,
,![]() 时,直接写出
时,直接写出![]() 的长.
的长.
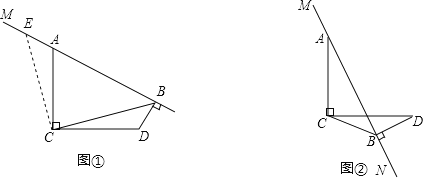
【答案】45;不改变,证明见解析;![]() 或
或![]() .
.
【解析】
[感知]证明△BCD≌△ECA(SAS)即可解决问题
[探究]结论不变,证明△BCD≌△ECA(SAS)即可解决问题.
[应用]分两种情形分别求解即可解决问题.
[感知],如图1中,在射线AM上截取AE=BD,连结CE.

∵AC⊥DC,DB⊥MN,
∴∠ACD=∠DBA=90°.
∴∠CDB+∠CAB=180°,
∵∠CAB+∠CAE=180°
∴∠D=∠CAE,∵CD=AC,AE=BD,
∴△BCD≌△ECA(SAS),
∴BC=EC,∠BCD=∠ECA,
∵∠ACE+∠ECD=90°,
∴∠ECD+∠DCB=90°,
即∠ECB=90°,
∴∠ABC=45°.
故答案为45
[探究]不改变.理由如下:
如图,如图2中,在射线AN上截取AE=BD,连接CE,设MN与CD交于点O.

∵AC⊥DC,DB⊥MN,
∴∠ACD=∠DBA=90°,
∵∠AOC=∠DOB,
∴∠D=∠EAC,CD=AC,
∴△BCD≌△ECA(SAS),
∴BC=EC,∠BCD=∠ECA,
∵∠ACE+∠ECD=90°,
∴∠ECD+∠DCB=90°,
即∠ECB=90°,
∴∠ABC=45°.
[拓展]如图①-1中,连接AD.

∴∠ACD+∠ABD=180°,
∴A,C,D,B四点共圆,
∴∠DAB=∠DCB=30°,
∴AB=![]() BD=
BD=![]() ,
,
∴EB=AE+AB=![]() +
+![]() ,
,
∵△ECB是等腰直角三角形,
∴BC=![]() .
.
如图②中,同法可得BC=![]() -1.
-1.
综上所述,BC的长为![]() +1或
+1或![]() -1.
-1.

 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
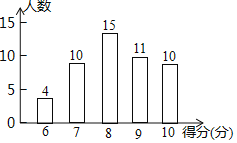
黄冈海淀全程培优测试卷系列答案【题目】如图所示的港珠澳大桥是目前桥梁设计中广泛采用的斜拉桥,它用粗大的钢索将桥面拉住,为检测钢索的抗拉强度,桥梁建设方从甲、乙两家生产钢索的厂方各随机选取5根钢索进行抗拉强度的检测,数据统计如下(单位:百吨)

甲、乙两厂钢索抗拉强度检测统计表
钢索 | 1 | 2 | 3 | 4 | 5 | 平均数 | 中位数 | 方差 |
甲厂 | 10 | 11 | 9 | 10 | 12 | 10.4 | 10 | 1.04 |
乙厂 | 10 | 8 | 12 | 7 | 13 | a | b | c |
(1)求乙厂5根钢索抗拉强度的平均数a(百吨)、中位数b(百吨)和方差c(平方百吨).
(2)桥梁建设方决定从抗拉强度的总体水平和稳定性来决定钢索的质量,问哪一家的钢索质量更优?