题目内容
(本小题满分7分)
向阳花卉基地出售两种花卉——百合和玫瑰,其单价为:玫瑰4元/株,百合5元/株,如果同一客户所购的玫瑰数量大于1200株,那么每株玫瑰还可降价1元。现某鲜花店向向阳花卉基地采购玫瑰1000株~1500株,百合若干株,此鲜花店本次用于采购玫瑰和百合恰好花去了9000元。然后再以玫瑰5元、百合6.5元的价格卖出。问:此鲜花店应如何采购这两种鲜花才能使获得的毛利润最大?
(注:1000株~1500株,表示大于或等于1000株,且小于或等于1500株。
毛利润=鲜花店卖出百合和玫瑰所获的总金额—购进百合和玫瑰的所需的总金额
采购百合900株,采购玫瑰1500株,毛利润最大为4350元
解析:解:设采购玫瑰x株,百合y株,毛利润为W元.
①当1000≤x≤1200时,
得4x+5y=9000,y=,
W=x+1.5y=2700-
当x取1000时,W有最大值2500.
②当1200<x≤1500时,
得3x+5y=9000,y=,
W=2x+1.5y=2x+1.5×=2700+
当x取1500时,W有最大值4350.
综上所述,采购玫瑰1500株,采购百合900株,毛利润最大为4350元.
答:采购百合900株,采购玫瑰1500株,毛利润最大为4350元.

 名校课堂系列答案
名校课堂系列答案(本小题满分12分)
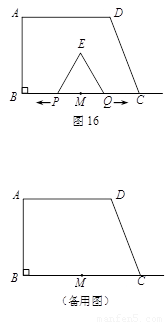
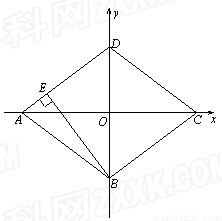
如图,在直角梯形ABCD中,AD∥BC,![]() ,AD = 6,BC = 8,
,AD = 6,BC = 8,![]() ,点M是BC的中点.点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动.在点P,Q的运动过程中,以PQ为边作等边三角形EPQ,使它与梯形ABCD在射线BC的同侧.点P,Q同时出发,当点P返回到点M时停止运动,点Q也随之停止.设点P,Q运动的时间是t秒(t>0).
,点M是BC的中点.点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动.在点P,Q的运动过程中,以PQ为边作等边三角形EPQ,使它与梯形ABCD在射线BC的同侧.点P,Q同时出发,当点P返回到点M时停止运动,点Q也随之停止.设点P,Q运动的时间是t秒(t>0).
 |
1.(1)设PQ的长为y,在点P从点M向点B运动的过程中,写出y与t之间的函数关系式(不必写t的取值范围).
2.(2)当BP = 1时,求△EPQ与梯形ABCD重叠部分的面积.
3.(3)随着时间t的变化,线段AD会有一部分被△EPQ覆盖,被覆盖线段的长度在某个时刻会达到最大值,请回答:该最大值能否持续一个时段?若能,直接写出t的取值范围;若不能,请说明理由.
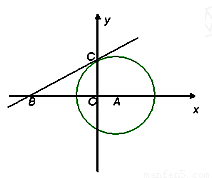
(本小题满分10分)已知:如图,⊙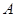 与
与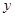 轴交于C、D两点,圆心
轴交于C、D两点,圆心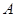 的坐标
的坐标
为(1,0),⊙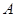 的半径为
的半径为 ,过点C作⊙
,过点C作⊙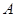 的切线交
的切线交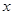 轴于点B(-4,0)
轴于点B(-4,0)
 |
1.(1)求切线BC的解析式;
2.(2)若点P是第一象限内⊙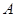 上一点,过点P作⊙A的切线与直线BC相交于点G,
上一点,过点P作⊙A的切线与直线BC相交于点G,
且∠CGP=120°,求点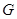 的坐标;
的坐标;
3.(3)向左移动⊙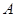 (圆心
(圆心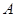 始终保持在
始终保持在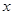 轴上),与直线BC交于E、F,在移动过程中是否存在点
轴上),与直线BC交于E、F,在移动过程中是否存在点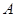 ,使得△AEF是直角三角形?若存在,求出点
,使得△AEF是直角三角形?若存在,求出点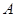 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
 的图像如图8所示,请将此图像向右平移1个单位,再向下平移2个单位.
的图像如图8所示,请将此图像向右平移1个单位,再向下平移2个单位.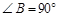 ,AD = 6,BC = 8,
,AD = 6,BC = 8,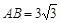 ,点M是BC的中点.点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动.在点P,Q的运动过程中,以PQ为边作等边三角形EPQ,使它与梯形ABCD在射线BC的同侧.点P,Q同时出发,当点P返回到点M时停止运动,点Q也随之停止.
,点M是BC的中点.点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动.在点P,Q的运动过程中,以PQ为边作等边三角形EPQ,使它与梯形ABCD在射线BC的同侧.点P,Q同时出发,当点P返回到点M时停止运动,点Q也随之停止.