Question

（本题满分9分）已知如图，矩形的长，宽，将沿翻折得．

（1）填空：度，点坐标为（　　，　　）；

（2）若两点在抛物线上，求的值，并说明点在此抛物线上；

（3）在（2）中的抛物线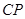段（不包括点）上，是否存在一点，使得四边形的面积最大？若存在，求出这个最大值及此时点的坐标；若不存在，请说明理由．

 

 

 

Answer 1

解：（1），　　··························································· 4分

 

（2）点，在抛物线上，

 

　　······················································ 2分

 

 

抛物线的解析式为　　······································ 1分

点坐标为    

 

点在此抛物线上．　　····························································· 1分

（3）假设存在这样的点，使得四边形的面积最大．

面积为定值，

要使四边形的面积最大，只需使的面积最大．

过点作轴分别交和轴于和，过点作轴交于．

 

设，

 

 

　　························································ 2分

 

，有最大值．

 

当时，的最大值是，

 

四边形的面积的最大值为．　　··································· 1分

 

此时点的坐标为．　　·················································· 1分

 

所以存在这样的点，使得四边形的面积最大，其最大值为．

 

解析:略