题目内容
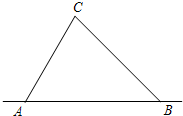 如图,我国海军为保卫海疆,在海岸线相距20海里的A、B处设立观测站(AB为直线),海岸线以外12海里范围内为我国领海,外国船只未经许可,不得私自进入.一天观测员发现一艘外国船只行驶至C处,在A处测得∠CAB为60°,在B处测得∠CBA为45°.通过计算说明观测员是否需要向未经许可的船只发出警告,令其退回?(
如图,我国海军为保卫海疆,在海岸线相距20海里的A、B处设立观测站(AB为直线),海岸线以外12海里范围内为我国领海,外国船只未经许可,不得私自进入.一天观测员发现一艘外国船只行驶至C处,在A处测得∠CAB为60°,在B处测得∠CBA为45°.通过计算说明观测员是否需要向未经许可的船只发出警告,令其退回?(| 2 |
| 3 |
分析:过点C作CD⊥AB,利用锐角三角函数求得CD的长后与12比较大小即可作出判断.
解答:解:过点C作CD⊥AB,垂足为D.设CD长为x海里.

∵∠CBA=45°,
∴∠DCB=45°,
∴CD=DB=x,
∵AB=20,
∴AD=20-x(2分)
又∵∠CAB=60°,
∴tan∠CAD=
,
则
=
,(5分)
解得x=30-10
≈13>12,(6分)
∴观测员不需要向未经许可的船只发出警告,令其退回.(7分)

∵∠CBA=45°,
∴∠DCB=45°,
∴CD=DB=x,
∵AB=20,
∴AD=20-x(2分)
又∵∠CAB=60°,
∴tan∠CAD=
| CD |
| AD |
则
| x |
| 20-x |
| 3 |
解得x=30-10
| 3 |
∴观测员不需要向未经许可的船只发出警告,令其退回.(7分)
点评:本题考查了解直角三角形的应用,解题的关键是正确的构造直角三角形并正确的解直角三角形.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
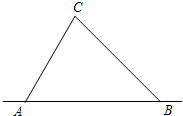 如图,我国海军为保卫海疆,在海岸线相距20海里的A、B处设立观测站(AB为直线),海岸线以外12海里范围内为我国领海,外国船只未经许可,不得私自进入.一天观测员发现一艘外国船只行驶至C处,在A处测得∠CAB为60°,在B处测得∠CBA为45°.通过计算说明观测员是否需要向未经许可的船只发出警告,令其退回?(
如图,我国海军为保卫海疆,在海岸线相距20海里的A、B处设立观测站(AB为直线),海岸线以外12海里范围内为我国领海,外国船只未经许可,不得私自进入.一天观测员发现一艘外国船只行驶至C处,在A处测得∠CAB为60°,在B处测得∠CBA为45°.通过计算说明观测员是否需要向未经许可的船只发出警告,令其退回?( 取1.4;
取1.4; 取1.7)
取1.7) 取1.4;
取1.4; 取1.7)
取1.7)