题目内容
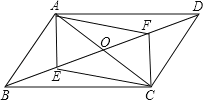
【题目】如图，在平行四边形ABCD中，AC=4，BD=6，P是BD上的任一点，过点P作EF∥AC，与平行四边形的两条边分别交于点E、F，设BP=x，EF=y，则能反映y与x之间关系的图象是（ ）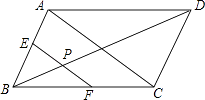 
A.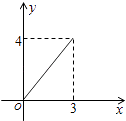
B.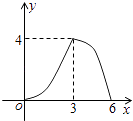
C.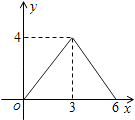
D.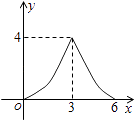
【答案】C
【解析】解：设AC交BD于O， ∵四边形ABCD是平行四边形，
∴OD=OB= 
BD=3，
当P在OB上时，
∵EF∥AC，
∴ 
= 
= 
，
∴ 
= 
，
∴y= 
x，
当P在OD上时，
同法可得： 
= 
= ，
∴ 
= ，
∴y=﹣ x+8，
∵两种情况都是一次函数，图象是直线．
故选：C．
根据平行四边形的性质得到OD=OB= BD=3，根据平行线分线段成比例定理得到 = 和 = ，代入求出y与x的关系式，根据函数的图象特点即可选出答案．
练习册系列答案
相关题目
