Question

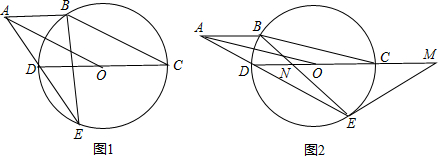
14．已知：CD为⊙O的直径，点B为⊙O上一点，ABCO为平行四边形，连接AD并延长交⊙O于点E，连接BE．
（1）在图1中，求证：∠DAO=∠BAO；
（2）在图1中，求证：BE=BC；
（3）在图2中，过点E作⊙O的切线交DC的延长线于点M，设BE，CD交于点N，若DE=EM，OM=8，求△BNC的面积．

Answer 1

分析 （1）证明AO⊥BD和△AFB≌△OFD，再利用线段垂直平分线的性质得：AD=OD，可得结论；
（2）设∠AOD=x°，则∠EDO=2x°，根据等腰三角形的性质得：∠OBE=∠OBC=∠BEO=∠C=x°，证明△BOE≌△BOC，则BE=BC；
（3）如图3，作辅助线，构建等边三角形的高线，利用面积法求高线CG的长，分别求BC的长，即是BE的长，利用线段的差计算EN的长，根据面积公式可得结论．

解答 证明：（1）如图1，连接BD，交AO于F，
∵四边形ABCO是平行四边形，
∴AB∥OC，AB=OC，
∴∠BAO=∠C=∠AOD，
∵DO=OC，
∴AB=DO，
∵∠AFB=∠OFD，
∴△AFB≌△OFD，
∴BF=DF，AF=OF，
∴OF⊥BD，
∴AD=OD，
∴∠DAO=∠AOD，
∴∠DAO=∠BAO；
（2）如图2，连接OB、OE，
设∠AOD=x°，则∠EDO=2x°，
∵OD=OE，
∴∠OED=∠EDO=2x°，
∵∠C=∠AOD=∠DEB=x°，
∴∠BEO=2x°-x°=x°，
∵OB=OC=OE，
∴∠OBE=∠OBC=∠BEO=∠C=x°，
∴△BOE≌△BOC，
∴BE=BC；
（3）如图3，连接OE、CE，
∵DE=EM，
由（2）知∠EDC=∠M=2x°，
∠MOE=2∠ODE=4x°，
∵ME是⊙O的切线，
∴OE⊥EM，
∴2x+4x=90，
x=15°，
∴∠M=30°，
∵OM=8，
∴OE=$\frac{1}{2}$OM=4，
∵OC=OE，∠COE=4×15°=60°，
∴△OEC是等边三角形，
∴EC=4，
过E作EH⊥DC于H，
∴∠HEC=30°，
∴HC=2，EH=2$\sqrt{3}$，
∵∠ONE=∠CDE+∠DEN=3x°=45°，
∴△NHE是等腰直角三角形，
∴NH=EH=2$\sqrt{3}$，
∴NE=2$\sqrt{6}$，
过C作CG⊥BE于G，
S_△ENC=$\frac{1}{2}$NC•EH=$\frac{1}{2}$EN•CG，
2$\sqrt{3}$（2+2$\sqrt{3}$）=2$\sqrt{6}$×CG，
CG=$\sqrt{6}$+$\sqrt{2}$，
Rt△BCG中，∠EBC=∠EDC=30°，
∴BC=2CG=2$\sqrt{6}+2\sqrt{2}$，
∴BE=BC=2$\sqrt{6}+2\sqrt{2}$，
∴BN=BE-EN=2$\sqrt{6}+2\sqrt{2}$-2$\sqrt{6}$=2$\sqrt{2}$，
∴S_△BNC=$\frac{1}{2}$BN•CG=$\frac{1}{2}$×2$\sqrt{2}$×$（\sqrt{6}+\sqrt{2}）$=2$\sqrt{3}$+2．

点评 本题是圆的综合题，考查了圆周角定理、切线的性质、等边三角形和等腰直角三角形的判定和性质、三角形全等的性质和判定、平行四这形的性质等知识，第三问有难度，确定计算面积的底边BN的长和高线CG的长是关键．