Question

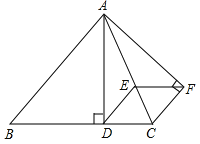
【题目】已知，为等边三角形，，为上一动点，以为边，如图所示作等边三角形，交于点，连接.

（1）求证：；

（2）若长为，长为，试求出与的函数关系.

Answer 1

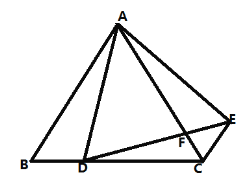
【答案】（1）证明见解析（2）

【解析】

（1）根据等边三角形的性质得到AB=AC，AD=AE，∠BAC=∠DAE，根据全等三角形的判定和性质即可得到结论；

（2）根据全等三角形的性质得到∠BAD=∠CAE，根据相似三角形的性质即可得到结论．

（1）证明：∵△ABC与△ADE是等边三角形，

∴AB=AC，AD=AE，∠BAC=∠DAE，

∴∠BAD=∠CAE，

在△ABD与△ACE中，

，

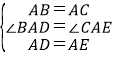∴△ABD≌△ACE，

∴BD=CE；

（2）∵△ABD≌△ACE，

∴∠BAD=∠CAE，

∵∠AED=∠ACB=60°，∠AFE=∠CFD，

∴∠CDF=∠CAE，

∴∠CDF=∠DAB，

∵∠B=∠DCF=60°，

∴△ABD∽△CDF，

∴ ，即，
∴y=-x2+x．