��Ŀ����
����Ŀ���Ķ����ϣ�
������������a��b����![]() �����ҽ���a��bʱȡ�Ⱥţ���
�����ҽ���a��bʱȡ�Ⱥţ���
��![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ����Сֵ����
����Сֵ����![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() �����ֵ��
�����ֵ��
���磺��֪![]() ����
����![]() ����
����![]() ����Сֵ��
����Сֵ��
�⣺��![]() ��
��![]() ����
����![]() ��
��![]() �����ҽ���
�����ҽ���![]() ��
��![]() ʱ��
ʱ��![]() ����Сֵ����СֵΪ
����Сֵ����СֵΪ![]() ��
��
����������Ķ����ϻش��������⣺
��1����֪![]() ����
����![]() ����
����![]() ��ʱ��
��ʱ��![]() ����Сֵ����СֵΪ ����
����Сֵ����СֵΪ ����
��2����֪![]() ����
����![]() ����
����![]() ȡ��ֵʱ��
ȡ��ֵʱ��![]() ����Сֵ����Сֵ�Ƕ��٣�
����Сֵ����Сֵ�Ƕ��٣�
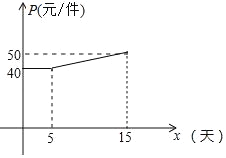
��3���ó�Ϊ![]() ���Χһ�������λ�������������λ��ij�������Ϊ����ʱ����Χ�ij����λ��������������Ƕ��٣�
���Χһ�������λ�������������λ��ij�������Ϊ����ʱ����Χ�ij����λ��������������Ƕ��٣�
���𰸡���1��![]() ��
��![]() ����2����
����2����![]()
![]() ʱ��
ʱ��![]() ����Сֵ����Сֵ��
����Сֵ����Сֵ��![]() ����3���������λ��ij�������Ϊ
����3���������λ��ij�������Ϊ![]() ʱ����Χ�ij����λ���������������
ʱ����Χ�ij����λ���������������![]() ��
��
��������
��1������![]() ������ֵ���ɵã�
������ֵ���ɵã�
��2���Ƚ�y����Ϊ![]() ���ٸ���
���ٸ���![]() ������ֵ���ɵã�
������ֵ���ɵã�
��3������������λ��ij�Ϊ![]() �����Ϊ
�����Ϊ![]() ���ٸ��ݳ����ε������ʽ�ɵ�
���ٸ��ݳ����ε������ʽ�ɵ�![]() ��Ȼ������
��Ȼ������![]() ������ֵ���ɵã�
������ֵ���ɵã�
��1����![]() ��
��![]()
���ҽ���![]() ����
����![]() ʱ��
ʱ��![]() ����Сֵ����СֵΪ12
����Сֵ����СֵΪ12
�ʴ�Ϊ��![]() ��12��
��12��
��2��![]()
![]()
��![]() ��
��![]()
���ҽ���![]() ����
����![]() ʱ��
ʱ��![]() ����Сֵ����СֵΪ9
����Сֵ����СֵΪ9
��![]() ʱ��
ʱ��![]() ����Сֵ����Сֵ��9��
����Сֵ����Сֵ��9��
��3������������λ��ij�Ϊ![]() �����Ϊ
�����Ϊ![]()
����Χ�ij����λ����Ϊ![]()
������ã�![]() ����
����![]()
��![]() ��
��![]() ����
����![]()
���ҽ���![]() ����
����![]() ʱ��
ʱ��![]() ȡ�����ֵ�����ֵΪ
ȡ�����ֵ�����ֵΪ![]()
��![]() ��
��![]() ʱ��
ʱ��![]() �����ֵ�����ֵΪ625
�����ֵ�����ֵΪ625
�𣺵������λ��ij�������Ϊ![]() ʱ����Χ�ij����λ���������������
ʱ����Χ�ij����λ���������������![]() ��
��

 ����������������ϵ�д�
����������������ϵ�д�