题目内容
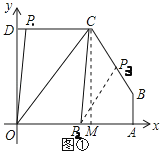
【题目】如图①,![]() ,
,![]() 分别在
分别在![]() 轴,
轴,![]() 轴上,
轴上,![]() 轴,
轴,![]() 轴.点
轴.点![]() 从点
从点![]() 出发,以1个单位长度/秒的速度,沿五边形
出发,以1个单位长度/秒的速度,沿五边形![]() 的边顺时针匀速运动一周,若顺次连接
的边顺时针匀速运动一周,若顺次连接![]() ,
,![]() ,
,![]() 三点所围成的三角形的面积为
三点所围成的三角形的面积为![]() ,点
,点![]() 运动的时间为
运动的时间为![]() 秒,已知
秒,已知![]() 与
与![]() 之间的函数关系如图②中折线
之间的函数关系如图②中折线![]() 所示.
所示.
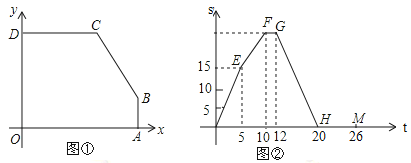
(1)图①中点![]() 的坐标为 ;点
的坐标为 ;点![]() 的坐标为 ;
的坐标为 ;
(2)求图②中![]() 所在直线的解析式;
所在直线的解析式;
(3)是否存在点![]() ,使
,使![]() 的面积为五边形
的面积为五边形![]() 的面积的
的面积的![]() ?若存在,请求出点
?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)(8,2),(5,6);(2)![]() ;(3)点
;(3)点![]() 的坐标为
的坐标为![]() ,或
,或![]() ,或
,或![]() ,或
,或![]() .
.
【解析】
(1)由于点P从点D出发,根据图②中S与t的图象可知,点P按顺时针方向沿五边形OABCD的边作匀速运动,又运动速度为1个单位长度/秒,所以DC=5,BC=5,AB=2,AO=8,OD=6,由此得到点C的坐标,由图②20-12=8,得出B的坐标;
(2)先求出点G坐标,再用待定系数法即可求出;
(3)先求出五边形OABCD的面积和△OCP的面积,再分类讨论三种情况:
①当P在CD上时,CP=5-t,由△OCP的面积得出t的值,即可得出P的坐标;
②当P在OA上时,设P(x,0),由△OCP的面积得出x的值,即可得出P的坐标;
③当P在BC上时,过点(![]() ,0)作OC平行线l交BC于P,求出直线OC和过点(
,0)作OC平行线l交BC于P,求出直线OC和过点(![]() ,0)与OC平行的直线l以及直线BC的解析式,l与BC的交点即为P,解方程组即可.
,0)与OC平行的直线l以及直线BC的解析式,l与BC的交点即为P,解方程组即可.
解:(1)由题意,可知点![]() 的运动路线是:
的运动路线是:![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ;
;
由图②:![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ;
;
(2)设![]() 的解析式为
的解析式为![]() ,
,
∵当点![]() 运动到
运动到![]() 时,
时,![]() ,
,
∴![]() ,
,
把点![]() ,
,![]() 代入得:
代入得:![]() ,
,
解得:![]() ,
,![]() ,
,
∴图②中![]() 所在直线的解析式为:
所在直线的解析式为:![]() ;
;
(3)存在点![]() ,使
,使![]() 的面积为五边形
的面积为五边形![]() 的面积的
的面积的![]() ;分三种情况:
;分三种情况:
作![]() 于
于![]() ,如图①所示:
,如图①所示:
则五边形![]() 的面积=矩形
的面积=矩形![]() 的面积+梯形
的面积+梯形![]() 的面积
的面积![]() ,
,
![]() 的面积
的面积![]() ,
,
分三种情况:
①由图象得:当![]() 在
在![]() 上时,
上时,![]() ,
,![]() 的面积
的面积![]() ,
,
解得:![]() ,
,
∴![]() ;
;
②由①得,当![]() 在
在![]() 上时,设
上时,设![]() ,
,
则![]() 的面积
的面积![]() ,
,
解得:![]() ,
,
∴![]() ;
;
③当![]() 在
在![]() 上时,过点
上时,过点![]() 作
作![]() 平行线
平行线![]() 交
交![]() 于
于![]() ;如图①所示:
;如图①所示:
∵直线![]() 为
为![]() ,设直线
,设直线![]() 的解析式为
的解析式为![]() ,
,
把点![]() 代入得:
代入得:![]() ,
,
∴![]() 的解析式为:
的解析式为:![]() ;
;
设直线![]() 的解析式为
的解析式为![]() ,
,
把![]() ,
,![]() 代入得:
代入得:![]() ,
,
解得:![]() ,
,![]() ,
,
∴直线![]() 的解析式为:
的解析式为:![]() ;
;
解方程组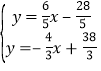 得:
得: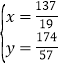 ,
,
∴![]() ;当
;当![]() 在
在![]() 上时,
上时,![]() ,
,![]() ,
,
∴![]() .
.
综上所述:点![]() 的坐标为
的坐标为![]() ,或
,或![]() ,或
,或![]() ,或
,或![]() .
.
故答案为:(1)(8,2),(5,6);(2)![]() ;(3)点
;(3)点![]() 的坐标为
的坐标为![]() ,或
,或![]() ,或
,或![]() ,或
,或![]() .
.

 阅读快车系列答案
阅读快车系列答案