题目内容
 如图,在x轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4,过点A1,A2,A3,A4分别作x轴的垂线与反比例函数y=
如图,在x轴的正半轴上依次截取OA1=A1A2=A2A3=A3A4,过点A1,A2,A3,A4分别作x轴的垂线与反比例函数y= 的图象相交于点P1,P2,P3,P4,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P4A4,并设其面积分别为S1,S2,S3,S4,则S4的值为________.
的图象相交于点P1,P2,P3,P4,得直角三角形OP1A1、A1P2A2、A2P3A3、A3P4A4,并设其面积分别为S1,S2,S3,S4,则S4的值为________.

分析:连接OP2,OP3,OP4,再根据反比例函数y=
 中k的几何意义进行解答即可.
中k的几何意义进行解答即可.解答:
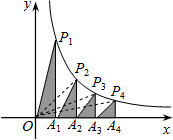 解:连接OP2,OP3,OP4,
解:连接OP2,OP3,OP4,∵P1,P2,P3,P4是反比例函数y=
 的图象上的点,A1P1、A2P2、A3P3、A4P4都垂直于x轴,
的图象上的点,A1P1、A2P2、A3P3、A4P4都垂直于x轴,∴S△A1P1O=S△A2P2O=S△A3P3O=S△A4P4O=
 ×2=1,
×2=1,∵OA1=A1A2=A2A3=A3A4,
∴S2=
 S1,S3=
S1,S3= S1,S4=
S1,S4= S1=
S1= ×1=
×1= .
.故答案为:
 .
.点评:本题考查的是反比例函数综合题,根据题意作出辅助线,利用反比例函数系数k的几何意义求解是解答此题的关键.

练习册系列答案
相关题目
 如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于A,B两点,点A在x轴的负半轴,点B在x轴的正半轴,与y轴交于点C,且tan∠ACO=
如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于A,B两点,点A在x轴的负半轴,点B在x轴的正半轴,与y轴交于点C,且tan∠ACO=| 1 |
| 2 |
| A、此抛物线的解析式为y=x2+x-2 | ||
| B、在此抛物线上的某点M,使△MAB的面积等于4,这样的点共有三个 | ||
C、此抛物线与直线y=-
| ||
| D、当x>0时,y随着x的增大而增大 |
 A在y轴的正半轴上,E是边AB上的一点,直线EC交y轴于F,且S△FAE:S四边形AOCE=1:3.
A在y轴的正半轴上,E是边AB上的一点,直线EC交y轴于F,且S△FAE:S四边形AOCE=1:3. A在y轴的正半轴上,E是边AB上的一点,直线EC交y轴于F,且S△FAE:S四边形AOCE=1:3.
A在y轴的正半轴上,E是边AB上的一点,直线EC交y轴于F,且S△FAE:S四边形AOCE=1:3. .
. 
