题目内容
如图，AD为△ABC的中线，BE为△ABD的中线。
1.∠ABE=15°，∠BAD=40°，求∠BED的度数；
2.在△BED中作BD边上的高，垂足为F；
3.若△ABC的面积为40，BD=5，则△BDE 中BD边上的高为多少？
1.∵∠ABE=15°，∠BAD=40°
∴∠BED=55°（2分）
2.
3.∵BD=5 AD为△ABC的中线∴BD=CD=5
∵△ABC的面积为40, ∴
BC×h=40
∴h=8 ∴△BDE面积为10，∴BD边上的高为5
解析:（1）根据三角形内角与外角的性质解答即可；
（2）过E作BC边的垂线即可；
（3）过A作BC边的垂线AG，再根据三角形中位线定理求解即可．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
相关题目
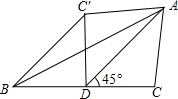如图，AD为△ABC的中线，∠ADC=45°，把△ADC沿AD对折，点C落在点C′的位置，BC=4，求BC′的长．
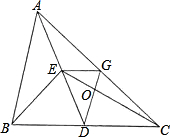如图，AD为△ABC的中线，BE为△ABD的中线．
如图，AD为△ABC的中线，BE为三角形ABD中线，
如图，AD为△ABC的中线，BE为△ABD的中线．
如图，AD为△ABC的中线，BE为△ABD的中线．