题目内容
一块三角形废料如图所示，∠C=90°，AC=8，BC=6．用这块废料剪出一个矩形CDEF，其中，点D、E、F分别在AC、AB、BC上．当AE为多长时使剪出的矩形CDEF面积最大，最大面积是多少？
解：∵∠C=90°，AC=8，BC=6，
∴AB=
=10，
∵四边形CDEF是矩形，
∴EF∥AC．
∴△BEF∽△BAC．
∴
．
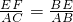设AE=x，则BE=10-x，
∴
，
∴EF=
（10-x），
同理：DE=
x，
矩形CDEF的面积S=DE•EF=x•（10-x）（0＜x＜10）
∴当x=5时，S有最大值为24．
分析：首先利用勾股定理求出AB的长，再根据四边形CDEF是矩形得到EF∥AC从而得到△BEF∽△BAC，设AE=x，则BE=10-x．利用相似三角形成比例表示出EF、DE，然后表示出有关x的二次函数，然后求二次函数的最值即可．
点评：本题考查了相似三角形的应用及二次函数的应用，解题的关键是从几何问题中整理出二次函数模型，并利用二次函数的知识求最值
∴AB=
=10，∵四边形CDEF是矩形，
∴EF∥AC．
∴△BEF∽△BAC．
∴
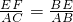．设AE=x，则BE=10-x，
∴
，∴EF=
（10-x），同理：DE=
x，矩形CDEF的面积S=DE•EF=
x•（10-x）（0＜x＜10）∴当x=5时，S有最大值为24．
分析：首先利用勾股定理求出AB的长，再根据四边形CDEF是矩形得到EF∥AC从而得到△BEF∽△BAC，设AE=x，则BE=10-x．利用相似三角形成比例表示出EF、DE，然后表示出有关x的二次函数，然后求二次函数的最值即可．
点评：本题考查了相似三角形的应用及二次函数的应用，解题的关键是从几何问题中整理出二次函数模型，并利用二次函数的知识求最值
练习册系列答案
相关题目
个平行四边形AGEF，其中，点G，E，F分别在AB，BC，AC上．设CE=x
（2012•和平区一模）一块三角形废料如图所示，∠A=30°，∠C=90°，AB=12．用这块废料剪出一个矩形CDEF，其中，点D、E、F分别在AC、AB、BC上．要使剪出的矩形CDEF面积最大，点E应选在何处？
（2012•道外区二模）一块三角形废料如图所示，∠A=30°，∠C=90°，AB=6米．用这块废料剪出一个矩形CDEF，其中点D、E、F分别在AC、AB、BC上、设边AE的长为x米，矩形CDEF的面积为S平方米．
一块三角形废料如图所示，∠A=30°，∠C=90°，AB=6米．用这块废料剪出一个矩形CDEF，其中点D、E、F分别在AC、AB、BC上、设边AE的长为x米，矩形CDEF的面积为S平方米．
时，y最大（小）值=
．