题目内容
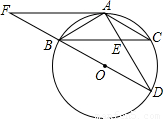
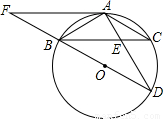
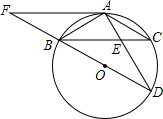如图，△ABC为圆O的内接三角形，BD为⊙O的直径，AB=AC，AD交BC于E，AE=2，ED=4．（1）求证：△ABE∽△ADB，并求AB的长；
（2）延长DB到F，使BF=BO，连接FA，那么直线FA与⊙O相切吗？为什么？
分析：（1）易得△ABE与△ADB的三个内角相等，故△ABE∽△ADB，进而可得
=
；代入数据可得答案．
（2）连接OA，根据勾股定理可得BF=BO=AB；易得∠OAF=90°，故可得直线FA与⊙O相切．
| AB |
| AD |
| AE |
| AB |
（2）连接OA，根据勾股定理可得BF=BO=AB；易得∠OAF=90°，故可得直线FA与⊙O相切．
解答：（1）证明：∵AB=AC，
∴∠ABC=∠C．
∵∠C=∠D，
∴∠ABC=∠D．
又∵∠BAE=∠DAB，
∴△ABE∽△ADB，（3分）
∴
=
，
∴AB2=AD•AE=（AE+ED）•AE=（2+4）×2=12，
∴AB=2
．（5分）
（2）解：直线FA与⊙O相切．（6分）
理由如下：
连接OA，
∵BD为⊙O的直径，
∴∠BAD=90°，
∴BD=
=
=
=4
，
∴BF=BO=
BD=
×4
=2
．
∵AB=2
，
∴BF=BO=AB，
∴∠OAF=90°．
∴直线FA与⊙O相切．（8分）
∴∠ABC=∠C．
∵∠C=∠D，
∴∠ABC=∠D．
又∵∠BAE=∠DAB，
∴△ABE∽△ADB，（3分）
∴
| AB |
| AD |
| AE |
| AB |
∴AB2=AD•AE=（AE+ED）•AE=（2+4）×2=12，
∴AB=2
| 3 |
（2）解：直线FA与⊙O相切．（6分）
理由如下：
连接OA，
∵BD为⊙O的直径，
∴∠BAD=90°，
∴BD=
| AB2+AD2 |
| 12+(2+4)2 |
| 48 |
| 3 |
∴BF=BO=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∵AB=2
| 3 |
∴BF=BO=AB，
∴∠OAF=90°．
∴直线FA与⊙O相切．（8分）
点评：本题考查常见的几何题型，包括切线的判定及相似三角形证明与性质的运用，要求学生掌握常见的解题方法，并能结合图形选择简单的方法解题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
