题目内容
【题目】如图, ![]() ,射线
,射线![]() ,且
,且![]() ,
, ![]() ,点
,点![]() 是线段
是线段![]() (不与点
(不与点![]() 、
、![]() 重合)上的动点,过点
重合)上的动点,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,连结
,连结![]() .
.
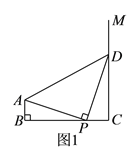
(![]() )如图
)如图![]() ,若
,若![]() ,求证:
,求证: ![]() ≌
≌![]() .
.
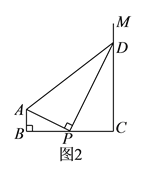
(![]() )如图
)如图![]() ,若
,若![]() 平分
平分![]() ,试猜测
,试猜测![]() 和
和![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
(![]() )若
)若![]() 是等腰三角形,作点
是等腰三角形,作点![]() 关于
关于![]() 的对称点
的对称点![]() ,连结
,连结![]() ,则
,则![]() __________.(请直接写出答案)
__________.(请直接写出答案)

【答案】(![]() )证明见解析; (
)证明见解析; (![]() )
)![]() ,理由见解析;(3)5.
,理由见解析;(3)5.
【解析】分析:(1)当BP=4时,CP=BC-BP=5=4=1,得出AB=PC,再根据AAS判定△APB≌△PDC;(2)先延长线段AP、DC交于点E,运用ASA判定△DPA≌△DPE,再运用AAS判定△APB≌△EPC,根据全等三角形的性质,即可得出结论;(3)先连接B'P,过点B'作B'F⊥CD于F,根据轴对称的性质,得出△ABP为等腰直角三角形,并判定四边形B'PCF是矩形,求得B'F=4,DF=3,最后在Rt△B'FD中,根据勾股定理即可求得B'D的长度.
本题解析:
证明:(![]() )∵
)∵![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
中,
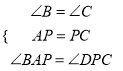 ,
,
∴![]() ≌
≌![]() .
.
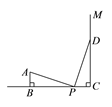
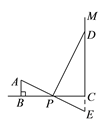
(![]() )过点
)过点![]() ,
, ![]() 交于
交于![]() 点,
点,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
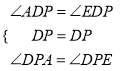 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
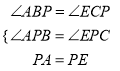 ,
,
∴![]() ≌
≌![]() ,
,
∴![]() .
.
(![]() )连接
)连接![]() ,作
,作![]() 于
于![]() 点,
点,
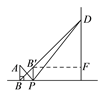
则![]() ,
,
∵![]() 是等腰三角形,
是等腰三角形,
∴![]() 为等腰直角三角形,即
为等腰直角三角形,即![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∵点![]() 关于
关于![]() 的对称点为
的对称点为![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
,
∴![]() 为等腰直角三角形,四边形
为等腰直角三角形,四边形![]() 是长方形,
是长方形,
∴![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
在![]() 中,
中, ![]() .
.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目