题目内容
 如图,在等腰△ABC中,AB=AC,B(
如图,在等腰△ABC中,AB=AC,B(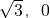 ),A(
),A( ).
).
(1)求点C的坐标;
(2)求△ABC的面积;
(3)如何平移△ABC,才能使A与原点O重合,并写出此时所得的三角形三个顶点的坐标.
解:(1)过A作AD⊥x轴于D,
∵AB=AC,
∴D为BC中点,
∵A( ),
),
∴OD=2 ,
,
∵B(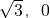 ),
),
∴OB= ,
,
∴BD=DC=2 -
- =
= ,
,
∴OC=OD+DC=2 +
+ =3
=3 ,
,
∴点C的坐标为(3 ,0)
,0)
(2)△ABC的面积: AD•BC=
AD•BC= ×
× ×
× =3;
=3;
(3)先向下平移 个长度单位,再向左平移2
个长度单位,再向左平移2 个长度单位.此时所得的三角形三个顶点的坐标分别为A(0,0),B(-
个长度单位.此时所得的三角形三个顶点的坐标分别为A(0,0),B(- ,-
,- ),C(
),C( ,-
,- ).
).
分析:(1)过A作AD⊥x轴于D,根据等腰三角形的性质即可求出点C的坐标;
(2)利用三角形的面积公式列式计算即可得解;
(3)根据平移中点的变化规律,求出点A、B、C的纵坐标即可得解.
点评:本题考查了等腰三角形的性质,三角形的面积和坐标与图形的性质-平移,熟记平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减是解题的关键.
∵AB=AC,
∴D为BC中点,
∵A(
 ),
),∴OD=2
 ,
,∵B(
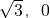 ),
),∴OB=
 ,
,∴BD=DC=2
 -
- =
= ,
,∴OC=OD+DC=2
 +
+ =3
=3 ,
,∴点C的坐标为(3
 ,0)
,0)(2)△ABC的面积:
 AD•BC=
AD•BC= ×
× ×
× =3;
=3;(3)先向下平移
 个长度单位,再向左平移2
个长度单位,再向左平移2 个长度单位.此时所得的三角形三个顶点的坐标分别为A(0,0),B(-
个长度单位.此时所得的三角形三个顶点的坐标分别为A(0,0),B(- ,-
,- ),C(
),C( ,-
,- ).
).分析:(1)过A作AD⊥x轴于D,根据等腰三角形的性质即可求出点C的坐标;
(2)利用三角形的面积公式列式计算即可得解;
(3)根据平移中点的变化规律,求出点A、B、C的纵坐标即可得解.
点评:本题考查了等腰三角形的性质,三角形的面积和坐标与图形的性质-平移,熟记平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减是解题的关键.

练习册系列答案
相关题目
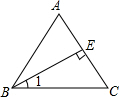 如图,在等腰△ABC中,AB=AC,BE⊥AC,垂足为E,则∠1与∠A的关系式为( )
如图,在等腰△ABC中,AB=AC,BE⊥AC,垂足为E,则∠1与∠A的关系式为( )| A、∠1=∠A | ||
B、∠1=
| ||
| C、∠1=2∠A | ||
| D、无法确定 |
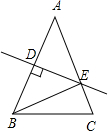 如图,在等腰△ABC中,AB=AC,AB的垂直平分线DE交AB于点D,交另一腰AC于点E,若∠EBC=15°,则∠A=
如图,在等腰△ABC中,AB=AC,AB的垂直平分线DE交AB于点D,交另一腰AC于点E,若∠EBC=15°,则∠A=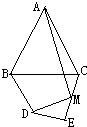 24、如图,在等腰△ABC中,AB=AC,∠ABC=α,在四边形BDEC中,DB=DE,∠BDE=2α,M为CE的中点,连接AM,DM.
24、如图,在等腰△ABC中,AB=AC,∠ABC=α,在四边形BDEC中,DB=DE,∠BDE=2α,M为CE的中点,连接AM,DM.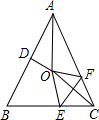 (2012•丽水)如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是
(2012•丽水)如图,在等腰△ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线交于点O,点C沿EF折叠后与点O重合,则∠CEF的度数是 如图,在等腰△ABC中,AB=AC=10cm,直线DE垂直平分AB,分别交AB、AC于D、E两点.若BC=8cm,则△BCE的周长是
如图,在等腰△ABC中,AB=AC=10cm,直线DE垂直平分AB,分别交AB、AC于D、E两点.若BC=8cm,则△BCE的周长是