题目内容
【题目】如图,在平面直角坐标系中,定点![]() 、
、![]() 、
、![]() 的坐标分别是(4,0)、(0,4)、(2,0),动点
的坐标分别是(4,0)、(0,4)、(2,0),动点![]() 在第一象限,且到原点
在第一象限,且到原点![]() 的距离为4个单位长度.
的距离为4个单位长度.
(1)当点![]() 到两坐标轴的距离相等时,求
到两坐标轴的距离相等时,求![]() 的面积;
的面积;
(2)若点![]() 是线段
是线段![]() (不与点
(不与点![]() 、
、![]() 重合)上的动点,当
重合)上的动点,当![]() 是等腰直角三角形时,求点
是等腰直角三角形时,求点![]() 到
到![]() 轴的距离.
轴的距离.


【答案】(1)![]() ;(2)点
;(2)点![]() 到
到![]() 轴的距离为
轴的距离为![]() 或
或![]() 或
或![]() .
.
【解析】
(1)利用三角形的面积公式直接计算即可;
(2)连接![]() ,设点
,设点![]() 到
到![]() 轴距离是
轴距离是![]() ,分三种情况讨论:①当
,分三种情况讨论:①当![]() 时,②当
时,②当![]() 时,③当
时,③当![]() 时,分别作出辅助线,构造全等三角形,利用勾股定理求解即可.
时,分别作出辅助线,构造全等三角形,利用勾股定理求解即可.
解:(1)∵点![]() 、
、![]() 、
、![]() 的坐标分别是(4,0)、(0,4)、(2,0),
的坐标分别是(4,0)、(0,4)、(2,0),
∴AC=2,
∴![]() ;
;
(2)连接![]() ,设点
,设点![]() 到
到![]() 轴距离是
轴距离是![]() ,
,
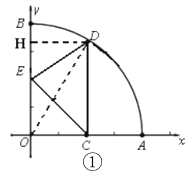
如图①,当![]() ,
,![]() 时,
时,
作![]() 于点
于点![]() ,
,
∵∠DHE=∠DEC=∠EOC=90°,
∴∠HDE+∠HED=∠HED+∠OEC,
∴∠HDE=∠OEC,
又∵DE=EC,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,![]() (舍去);
(舍去);
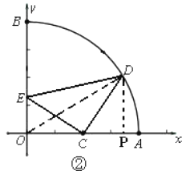
如图②,当![]() ,
,![]() ,
,
作![]() ,同理可得
,同理可得![]() ,
,
则![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,![]() (舍去);
(舍去);
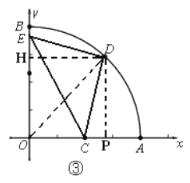
如图③,当![]() ,
,![]() 时,
时,
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,同理可得
,同理可得![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() (舍去),
(舍去),
综上所述,当![]() 为等腰直角三角形时,点
为等腰直角三角形时,点![]() 到
到![]() 轴的距离为
轴的距离为![]() 或
或![]() 或
或![]() .
.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目








