题目内容
下列说法
①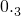 是分数;
是分数;
②正数不一定是有理数;
③互为相反数的两个数的商为-1;
④若ab>0且a>b,则 ,
,
其中正确的是
- A.①②③
- B.①②④
- C.②③④
- D.①③④
B
分析:①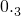 是无限循环小数,能化为分数,本选项正确;②正数不一定是有理数,可以举一个反例说明一下;③互为相反数的两个数的商为-1是错误的,0和0互为相反数,其商没有意义;④若ab>0,得到a与b同号,故在a>b左右两边同时除以ab,化简后即可得到
是无限循环小数,能化为分数,本选项正确;②正数不一定是有理数,可以举一个反例说明一下;③互为相反数的两个数的商为-1是错误的,0和0互为相反数,其商没有意义;④若ab>0,得到a与b同号,故在a>b左右两边同时除以ab,化简后即可得到 ,本选项正确.
,本选项正确.
解答:①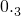 =
= ,故
,故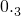 是分数,本选项正确;
是分数,本选项正确;
②正数不一定是有理数,例如π>0是正数,但不是有理数;
③互为相反数的两个数的商不一定为-1,例如0和0互为相反数,但是商没有意义;
④∵ab>0,∴a与b同号,
又a>b,∴不等式左右两边同时除以ab得: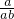 >
>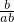 ,即
,即 ,本选项正确,
,本选项正确,
则正确的选项有:①②④.
故选B.
点评:此题考查了有理数的混合运算,涉及到的知识有:有理数的分类,无限循环小数属于分数,有理数的定义,互为相反数的两数满足的特点,两数相乘的取符合法则,以及不等式的基本性质,扎实掌握基本概念,灵活意义所学知识是解本题的关键.
分析:①
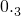 是无限循环小数,能化为分数,本选项正确;②正数不一定是有理数,可以举一个反例说明一下;③互为相反数的两个数的商为-1是错误的,0和0互为相反数,其商没有意义;④若ab>0,得到a与b同号,故在a>b左右两边同时除以ab,化简后即可得到
是无限循环小数,能化为分数,本选项正确;②正数不一定是有理数,可以举一个反例说明一下;③互为相反数的两个数的商为-1是错误的,0和0互为相反数,其商没有意义;④若ab>0,得到a与b同号,故在a>b左右两边同时除以ab,化简后即可得到 ,本选项正确.
,本选项正确.解答:①
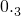 =
= ,故
,故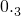 是分数,本选项正确;
是分数,本选项正确;②正数不一定是有理数,例如π>0是正数,但不是有理数;
③互为相反数的两个数的商不一定为-1,例如0和0互为相反数,但是商没有意义;
④∵ab>0,∴a与b同号,
又a>b,∴不等式左右两边同时除以ab得:
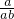 >
>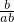 ,即
,即 ,本选项正确,
,本选项正确,则正确的选项有:①②④.
故选B.
点评:此题考查了有理数的混合运算,涉及到的知识有:有理数的分类,无限循环小数属于分数,有理数的定义,互为相反数的两数满足的特点,两数相乘的取符合法则,以及不等式的基本性质,扎实掌握基本概念,灵活意义所学知识是解本题的关键.

练习册系列答案
相关题目