题目内容

如图，点M是反比例函数y= $数学公式$ （x＞0）图象上的一个动点，过点M作x的平行线交反比例函数y=- $数学公式$ （x＜0）图象于点N．
（1）若点M的坐标为（1，5），则点N的坐标为______；
（2）若点P是x上的任意一点，则△PMN的面积是否发生变化？请说明理由．

解：（1）点N的坐标为（-1，5）；

（2）△PMN的面积不会发生变化．理由是：
设点M的坐标为（a， $\text{[math]}$ ），
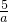当y= 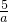$\text{[math]}$ 时，- $\text{[math]}$ = $\text{[math]}$ ，
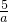解得x=-a，
即点N的坐标为（-a， $\text{[math]}$ ），
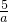∴MN=a-（-a）=2a，
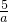∴S_△PMN= $\text{[math]}$ MN•h= $\text{[math]}$ ×2a× $\text{[math]}$ =5．
∴△PMN的面积不会发生变化．
第（2）小题另解的思路：（2）△PMN的面积不会发生变化．
理由是：如右图，过点N作NA∥MP，NB⊥x轴，MC⊥x轴，

易证得：四边形NAPM是平行四边形，
四边形NBCM是矩形．
∵点M、N分别在反比例函数y= $\text{[math]}$ 与y=- $\text{[math]}$ 的图象上，
∴S_矩形NBCM=2×5=10，
∴S_△PMN= $\text{[math]}$ S_{四边形NAPM}= $\text{[math]}$ S_矩形NBCM=5，
∴△PMN的面积不会发生变化．
分析：（1）M与N关于y轴对称，利用对称点的坐标的关系即可求解；
（2）点M的坐标为（a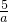， $\text{[math]}$ ），即可求得N的坐标，则MN的长度可以利用a表示，M点的纵坐标的值就是MN边上的高，然后利用三角形的面积公式即可表示出△MNP的面积，从而判断面积是否与a的值有关．从而判断△PMN的面积是否发生变化．
点评：本题考查反比例函数系数k的几何意义，过双曲线上的任意一点分别向两条坐标轴作垂线，与坐标轴围成的矩形面积就等于|k|．本知识点是中考的重要考点，同学们应高度关注．