Question

观察图中给出的直线y=k₁x+b和反比例函数y=

k2

x

的图象，判断下列结论错误的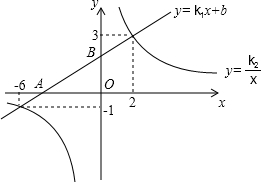有（　　）
①k₂＞b＞k₁＞0；②直线y=k₁x+b与坐标轴围成的△ABO的面积是4；
③方程组

y=k1x+b y= k2 x

的解为

x1=-6 y1=-1

，

x2=2 y2=3

；
④当-6＜x＜2时，有k₁x+b＞

k2

x

．

• A、1个
• B、2个
• C、3个
• D、4个

Answer 1

分析：①利用待定系数法分别求出直线y=k₁x+b和反比例函数y=

k2

x

的解析式，从而可知k₂、b、k₁、0的大小关系；
②根据直线y=k₁x+b的解析式，首先求出A与B的坐标，然后由三角形的面积公式可求出△ABO的面积；
③观察直线y=k₁x+b和反比例函数y=

k2

x

的图象的交点坐标，即可判定方程组

y=k1x+b y= k2 x

的解是否正确；
④观察直线y=k₁x+b位于反比例函数y=

k2

x

的图象上方的部分对应的x的取值，即可判断是否正确．

解答：解：①∵反比例函数y=

k2

x

的图象经过点（2，3），
∴k₂=2×3=6，
∴y=

6

x

．
∵直线y=k₁x+b经过点（2，3）和点（-6，-1），
∴

2k1+b=3 -6k1+b=-1

，
∴

k1= 1 2 b=2

，
∴y=

1

2

x+2．
∴k₂＞b＞k₁＞0，正确；
②∵y=

1

2

x+2，
∴当y=0，x=-4．∴点A的坐标是（-4，0），
当x=0时，y=2．∴点B的坐标是（0，2）．
∴△ABO的面积是

1

2

×4×2=4，正确；
③观察图象，发现直线y=k₁x+b和反比例函数y=

k2

x

的图象交于点（-6，-1），（2，3），则方程组

y=k1x+b y= k2 x

的解为

x1=-6 y1=-1

，

x2=2 y2=3

，正确；
④观察图象，可知当-6＜x＜0或x＞2时，有k₁x+b＞

k2

x

，错误．
故选A．

点评：本题考查了用待定系数法求函数的解析式，求三角形的面积，函数图象与方程组的解的关系，体现了数形结合的思想．