题目内容
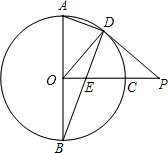 如图,AB为⊙O的直径,且OC⊥AB,P为OC的延长线上一点,PD切⊙O于点D,BD交OC于点E,若AB=6,PD=4,则DE的长为
如图,AB为⊙O的直径,且OC⊥AB,P为OC的延长线上一点,PD切⊙O于点D,BD交OC于点E,若AB=6,PD=4,则DE的长为
- A.

- B.

- C.

- D.
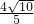
D
分析:AB为⊙O的直径,即△ADB为Rt△,先根据切线长定理可得出PC的长,又OD⊥PD,可得PC的值;又∠PDB=∠A,且易得∠AOD=∠P,可证△PDE∽△OAD,可证PE=PD,可得出PE的值;即可得出OE的值,在Rt△OEB中,可得出BE的值,利用相交弦定理即可得出DE的值.
解答:根据题意可得,∠PDB=∠A,
且∠P+∠DOP=90°,∠AOD+∠DOP=90°,
即可得出∠AOD=∠P,
得证△AOD∽△DPE,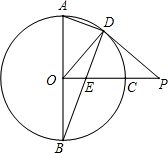
即有PE=PD=4,
又OD⊥PD,
即可得出PO=5,即CE=2,
在Rt△BOE,可得出
BE= ,
,
又BE•DE=CE•(CE+OC);
可得出DE=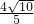 .
.
即答案为: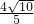 .
.
点评:本题主要考查了切线的性质、相交弦定理以及解直角三角形等知识点,本题有一定难度,希望学生能够仔细分析题意,认真完成题目.
分析:AB为⊙O的直径,即△ADB为Rt△,先根据切线长定理可得出PC的长,又OD⊥PD,可得PC的值;又∠PDB=∠A,且易得∠AOD=∠P,可证△PDE∽△OAD,可证PE=PD,可得出PE的值;即可得出OE的值,在Rt△OEB中,可得出BE的值,利用相交弦定理即可得出DE的值.
解答:根据题意可得,∠PDB=∠A,
且∠P+∠DOP=90°,∠AOD+∠DOP=90°,
即可得出∠AOD=∠P,
得证△AOD∽△DPE,

即有PE=PD=4,
又OD⊥PD,
即可得出PO=5,即CE=2,
在Rt△BOE,可得出
BE=
 ,
,又BE•DE=CE•(CE+OC);
可得出DE=
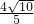 .
.即答案为:
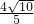 .
.点评:本题主要考查了切线的性质、相交弦定理以及解直角三角形等知识点,本题有一定难度,希望学生能够仔细分析题意,认真完成题目.

练习册系列答案
相关题目
 如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为( )
如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为( )| A、1cm | B、2cm | C、3cm | D、4cm |
 如图,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,则水管的长为
如图,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,则水管的长为
 如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为
如图,已知⊙O的直AB=20cm,CD垂AB于E,CD=12cm,AE的长为