题目内容
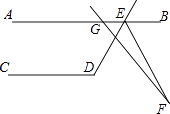
【题目】如图,半径OA=2cm,圆心角为90°的扇形OAB中,C为 ![]() 的中点,D为OB的中点,则图中阴影部分的面积为cm2 .
的中点,D为OB的中点,则图中阴影部分的面积为cm2 . 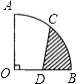
【答案】![]() (π﹣
(π﹣ ![]() )
)
【解析】解:连接CO, 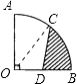
易得∠COB=45°.
作CE⊥OB于点E,
那么CE=CO×sin45°= ![]() .
.
阴影部分面积=S扇形BOC﹣S△OCD= ![]() ﹣
﹣ ![]() ×1×
×1× ![]() =
= ![]() (π﹣
(π﹣ ![]() ).
).
【考点精析】解答此题的关键在于理解扇形面积计算公式的相关知识,掌握在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2),以及对解直角三角形的理解,了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).

练习册系列答案
相关题目