题目内容
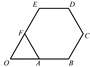
【题目】如图，正六边形ABCDEF的边长为
，延长BA，EF交于点O.以O为原点，以边AB所在的直线为
轴建立平面直角坐标系，则直线DF与直线AE的交点坐标是(_______).
【答案】（2
,4）
【解析】试题解析：如答图，连接AE，DF，
∵正六边形ABCDEF的边长为
，延长BA，EF交于点O，
∴△AOF是等边三角形，则AO=FO=FA=
.
∵以O为原点，以边AB所在的直线为x轴建立平面直角坐标系，∠EOA=60°，EO=FO+EF=
，
∴∠EAO=90°，∠OEA=30°．∴AE=
cos30°=6．∴F（
，3），D（
，6）．
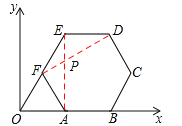
设直线DF的解析式为：y=kx+b，
则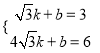
，解得：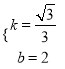 
.
∴直线DF的解析式为： 
.
∵当x=
时， 
，
∴直线DF与直线AE的交点坐标是：（
，4）．
故答案为：（
，4）．
练习册系列答案
相关题目
