题目内容
)如图，AB是半圆O的直径，点C是⊙O上一点（不与A，B重合），连接AC，BC，过点O作OD∥AC交BC于点D，在OD的延长线上取一点E，连接EB，使∠OEB=∠ABC.
(1)求证：BE是⊙O的切线；
(2)若OA=10，BC=16，求BE的长.
 |
证明：（1）∵AB是半圆O的直径， ∴∠ACB=90°， 1分
∵OD∥AC， ∴∠ODB=90°， ∴∠EDB=90°，1分
∴∠OEB+∠DBE=90°， 而∠OEB=∠ABC，∴∠ABC+∠DBE=90°，
∴∠ABE=90°，∴BE⊥AB 2分，
∴ BE是⊙O的切线 2分
（2）由（1）知道△ABC是直角三角形，∴AC=12 1分
中位线定理可知 OD＝6 1 分 勾股得DB=8 1分
设DE=x，根据勾股得
即
解得x=
2分 根据勾股得 BE=
1分
练习册系列答案
相关题目
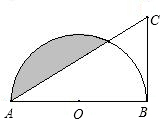如图，AB是半圆O的直径，∠BAC=30°，BC为半圆的切线，切点为B，且BC=4\sqrt{3}．
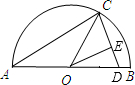如图，AB是半圆O的直径，AC=AD，OC=2，∠CAB=30°，则点O到CD的距离OE=
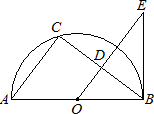AC交BC于点D，在OD的延长线上取一点E，连接EB，使∠OEB=∠ABC．
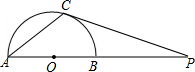（2013•镇江）如图，AB是半圆O的直径，点P在AB的延长线上，PC切半圆O于点C，连接AC．若∠CPA=20°，则∠A=