��Ŀ����
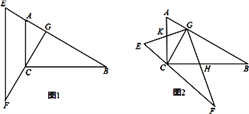
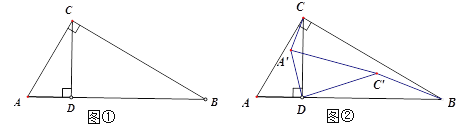
����Ŀ����ͼ�٣���Rt��ABC�У���C=90��, ��B=30��,AC=1,CD��AB������ΪD���ֽ���ACD��D��˳ʱ����ת![]() �õ���A��C��D, ��תʱ��Ϊt�룬��ACD��D����ת�Ľ��ٶ�
�õ���A��C��D, ��תʱ��Ϊt�룬��ACD��D����ת�Ľ��ٶ�![]() /��(ÿ��ת10��) ��
/��(ÿ��ת10��) ��
��1����תʱ��t= ��ʱ��A��C����AB;
��2����ACD��D��˳ʱ����תһ�ܣ�3600����б��ACɨ�������Ϊ ��
��3����ͼ�ڣ�����A��C�� C��B��
����6��t��9����֤�� ![]() Ϊ��ֵ��
Ϊ��ֵ��
�ڵ�t��9ʱ���������ۻ������������ֱ��д����ֵ����������˵�����ɣ�
���𰸡���1��6��2��![]() ��3����֤�����������ڽ��۳�������ֵ��Ϊ
��3����֤�����������ڽ��۳�������ֵ��Ϊ![]() .
.
����������������1������ת����ת�ɵ���Ҫ![]() ��AB,��
��AB,��![]() ,������⣻��2���������֪б��ACɨ�������Ϊ�Ե�DΪԲ��CD��AC���ϵĸ�Ϊ�뾶�Ļ��Σ����ô�Բ�����ȥСԲ���������⣻��3���ٵ�6��t��9ʱ��֪60�㣼����90�㣬�ɡ�
,������⣻��2���������֪б��ACɨ�������Ϊ�Ե�DΪԲ��CD��AC���ϵĸ�Ϊ�뾶�Ļ��Σ����ô�Բ�����ȥСԲ���������⣻��3���ٵ�6��t��9ʱ��֪60�㣼����90�㣬�ɡ�![]() �ס�
�ס�![]() �͡�
�͡�![]() �ס�
�ס�![]() �õ�
�õ�![]() Ϊ��ֵ
Ϊ��ֵ![]() �����������ͬ�ķ������ɵó����.
�����������ͬ�ķ������ɵó����.
���������
��1����![]() ��AB,��
��AB,��![]() ����t=6.
����t=6.
��2����AC���ϵĸ�Ϊh,��![]() .
.
��3���ٵ�6��t��9ʱ��֪600��![]() ��900
��900
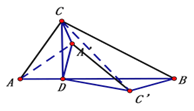
��ͼ����AA����C C��
����ת����֪
��AD A��=��CD C��=��![]()
��AD=A��D��CD= C��D
���ADA�� �ס�C D C����
���A��A D =��C��CD ; ![]() ,
,
�֡ߡ�CAD =��BCD =60O
���ACA�� �ס�C BC��
��![]() Ϊ��ֵ.
Ϊ��ֵ.
�ڽ��۳�������ֵ��Ϊ![]() .
.

����Ŀ�����ݺͺ���ij��ͬʱ����ij���ͺŵĻ�������̨�����ݳ���֧Ԯ���![]() ̨�����ݳ���֧Ԯ���
̨�����ݳ���֧Ԯ���![]() ̨�����ھ������人
̨�����ھ������人![]() ̨���ϲ�
̨���ϲ�![]() ̨��ÿ̨�������˷ѣ���λ����Ԫ��������躼�������ϲ��Ļ���Ϊ
̨��ÿ̨�������˷ѣ���λ����Ԫ��������躼�������ϲ��Ļ���Ϊ![]() ̨��
̨��
�ϲ� | �人 | |
���ݳ� |
|
|
���ݳ� |
|
|
��![]() ����
����![]() �Ĵ���ʽ����ʾ���˷ѣ���λ����Ԫ����
�Ĵ���ʽ����ʾ���˷ѣ���λ����Ԫ����
��![]() �������˷�Ϊ
�������˷�Ϊ![]() Ԫ�����������ϲ��Ļ���ӦΪ����̨?
Ԫ�����������ϲ��Ļ���ӦΪ����̨?
��![]() ������������ʹ���˷���
������������ʹ���˷���![]() Ԫ?���п��ܣ���д����Ӧ�ĵ��˷����������ܣ���˵�����ɣ�
Ԫ?���п��ܣ���д����Ӧ�ĵ��˷����������ܣ���˵�����ɣ�