题目内容
已知Rt△ABC,∠C=90°,
若∠A=30°,BC=2,则AB=________,AC=________;
若∠A=30°,AB=2,则BC=________,AC=________;
若∠A=30°,AC=2,则AB=________,BC=________.
4 2 1
1 


分析:先根据含30度角的直角三角形性质求出BC,根据勾股定理求出AC即可,也可以解直角三角形求出各个边的长度.
解答:
∵∠C=90°,∠A=30°,BC=2,
∴AB=2BC=4,
由勾股定理得:AC= ;
;
∵∠C=90°,∠A=30°,AB=2,
∴BC= AB=1,
AB=1,
由勾股定理得:AC= =
= ;
;
∵∠C=90°,∠A=30°,AC=2,
∴BC= =
= ,AB=2BC=
,AB=2BC= ;
;
故答案为:4,2 ,1,
,1, ,
, ,
, .
.
点评:本题考查了含30度角的直角三角形,勾股定理,解直角三角形的应用,主要考查学生的计算能力.
 1
1 


分析:先根据含30度角的直角三角形性质求出BC,根据勾股定理求出AC即可,也可以解直角三角形求出各个边的长度.
解答:

∵∠C=90°,∠A=30°,BC=2,
∴AB=2BC=4,
由勾股定理得:AC=
 ;
;∵∠C=90°,∠A=30°,AB=2,
∴BC=
 AB=1,
AB=1,由勾股定理得:AC=
 =
= ;
;∵∠C=90°,∠A=30°,AC=2,
∴BC=
 =
= ,AB=2BC=
,AB=2BC= ;
;故答案为:4,2
 ,1,
,1, ,
, ,
, .
.点评:本题考查了含30度角的直角三角形,勾股定理,解直角三角形的应用,主要考查学生的计算能力.

练习册系列答案
相关题目
已知Rt△ABC中,∠C=90°,AC=8cm,BC=6cm.则其内心和外心之间的距离是( )
| A、10cm | ||
| B、5cm | ||
C、
| ||
| D、2cm |
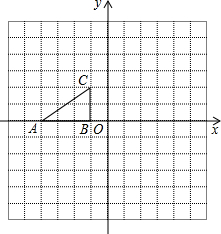 如图,每个小方格都是边长为1个单位的正方形.Rt△ABC 的顶点在格 点上,建立平面直角坐标系后,点A的坐标为(-4,0),点B的坐标为(-1,0).已知Rt△ABC和Rt△A1B1C1关于y轴对称,Rt△A1B1C1和Rt△A2B2C2关于直线y=-2轴对称.
如图,每个小方格都是边长为1个单位的正方形.Rt△ABC 的顶点在格 点上,建立平面直角坐标系后,点A的坐标为(-4,0),点B的坐标为(-1,0).已知Rt△ABC和Rt△A1B1C1关于y轴对称,Rt△A1B1C1和Rt△A2B2C2关于直线y=-2轴对称.