题目内容
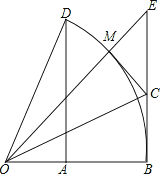
【题目】如图,以O为圆心的弧![]() 度数为60°,∠BOE=45°,DA⊥OB,EB⊥OB.
度数为60°,∠BOE=45°,DA⊥OB,EB⊥OB.
(1)求![]() 的值;
的值;
(2)若OE与![]() 交于点M,OC平分∠BOE,连接CM.说明CM为⊙O的切线;
交于点M,OC平分∠BOE,连接CM.说明CM为⊙O的切线;
(3)在(2)的条件下,若BC=1,求tan∠BCO的值.
【答案】(1)![]() ;(2)理由见解析;(3)
;(2)理由见解析;(3)![]() +1.
+1.
【解析】
试题分析:(1)求出OB=BE,在Rt△OAD中,sin∠AOD=![]() ,代入求出即可;
,代入求出即可;
(2)求出∠BOC=∠MOC,证△BOC≌△MOC,推出∠CMO=∠OBC=90°,根据切线的判定推出即可;
(3)求出CM=ME,MC=BC,求出BC=MC=ME=1,在Rt△MCE中,根据勾股定理求出CE=![]() ,求出OB=
,求出OB=![]() +1,解直角三角形得出tan∠BCO=
+1,解直角三角形得出tan∠BCO=![]() +1,即可得出答案.
+1,即可得出答案.
试题解析:(1)∵EB⊥OB,∠BOE=45°,
∴∠E=45°,
∴∠E=∠BOE,
∴OB=BE,
在Rt△OAD中,sin∠AOD=![]() ,
,
∵OD=OB=BE,
∴![]() ;
;
(2)∵OC平分∠BOE,
∴∠BOC=∠MOC,
在△BOC和△MOC中,
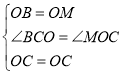
∴△BOC≌△MOC(SAS),
∴∠CMO=∠OBC=90°,
又∵CM过半径OM的外端,
∴CM为⊙O的切线;
(3)由(1)(2)证明知∠E=45°,OB=BE,△BOC≌△MOC,CM⊥ME,
∵CM⊥OE,∠E=45°,
∴∠MCE=∠E=45°,
∴CM=ME,
又∵△BOC≌△MOC,
∴MC=BC,
∴BC=MC=ME=1,
∵MC=ME=1,
∴在Rt△MCE中,根据勾股定理,得CE=![]() ,
,
∴OB=BE=![]() +1,
+1,
∵tan∠BCO=![]() ,OB=
,OB=![]() +1,BC=1,
+1,BC=1,
∴tan∠BCO=![]() +1.
+1.

练习册系列答案
相关题目