题目内容
等腰三角形一腰上的高与另一腰的夹角为30°，腰长为2，则其底边的高为分析：结合题意，画出图形，当腰上的高在两腰之间时，可得该三角形为等边三角形，可得腰上的高等于底边的上的高，即可得底边上的高为1；当腰上的高在外侧时，可得底边上的高为
．
| 3 |
解答：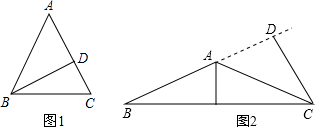
解：①如图1，已知AB=AC=2，BD为腰AC上的高，可知∠ABD=30°，可得∠A=60°，即证△ABC为正三角形，即可得出底边AC上的高等于腰上的高等于
．
②如图2，AB=AC=2，CD⊥BA交BA是延长线于点D，且∠CAD=30°，可得AD=1，CD=
，
可得BC=2
，即BE=
，在Rt△ABE中，AB=2，BE=
，即AE=1．
故答案为：1或
．
解：①如图1，已知AB=AC=2，BD为腰AC上的高，可知∠ABD=30°，可得∠A=60°，即证△ABC为正三角形，即可得出底边AC上的高等于腰上的高等于| 3 |
②如图2，AB=AC=2，CD⊥BA交BA是延长线于点D，且∠CAD=30°，可得AD=1，CD=
| 3 |
可得BC=2
| 3 |
| 3 |
| 3 |
故答案为：1或
| 3 |
点评：本题主要考查的是利用等腰三角形的性质解直角三角形．
练习册系列答案
名校课堂系列答案
相关题目