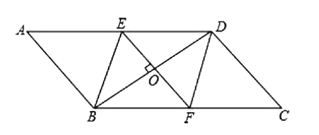
题目内容
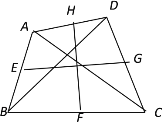
【题目】如图,在![]() 是平行四边形
是平行四边形![]() 的对角线
的对角线![]() 的垂直平分线,
的垂直平分线,![]() 与边
与边![]() 分别交于点
分别交于点![]() 。
。
(1)求证:四边形![]() 是菱形;
是菱形;
(2)若![]() ,求菱形
,求菱形![]() 的面积。
的面积。
【答案】(1)见解析;(2)24.
【解析】
(1)根据平行四边形ABCD的性质得到![]() ,利用“ASA”得到
,利用“ASA”得到![]() ,根据全等三角形的对应边相等得到
,根据全等三角形的对应边相等得到![]() ,由一组对边平行且相等的四边形为平行四边形得到四边形
,由一组对边平行且相等的四边形为平行四边形得到四边形![]() 是平行四边形,又根据对角线垂直的平行四边形为菱形即可得证;
是平行四边形,又根据对角线垂直的平行四边形为菱形即可得证;
(2)由菱形性质求得OD的长度,利用勾股定理求得OE的长度,进而求EF的长,而BD与EF为菱形BFDE的两条对角线,根据对角线乘积的一半即可求出菱形的面积.
解:(1)∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∵![]() ,
,
∴![]() 是菱形.
是菱形.
(2)∵![]() 是菱形
是菱形
∴![]() ,
,![]()
∴在Rt△EOD中,![]()
所以EF=6
∴菱形![]() 的面积为:
的面积为:![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目