题目内容
阅读材料:如果一元二次方程ax2+bx+c=0(a≠0)的两个实数根分别是x1、x2,那么x1+x2=-
,x1•x2=
.借助该材料完成下列各题:
(1)若x1、x2是方程x2-4x+
=0的两个实数根,x1+x2=
.
(2)若x1、x2是方程2x2+6x-3=0的两个实数根,
+
=
+
=
(3)若x1、x2是关于x的方程x2-(m-3)x+m+8=0的两个实数根,且
+
=13,求m的值.
| b |
| a |
| c |
| a |
(1)若x1、x2是方程x2-4x+
| 5 |
4
4
;x1•x2=| 5 |
| 5 |
(2)若x1、x2是方程2x2+6x-3=0的两个实数根,
| 1 |
| x1 |
| 1 |
| x2 |
-2
-2
;| x | 2 1 |
| x | 2 2 |
12
12
.(3)若x1、x2是关于x的方程x2-(m-3)x+m+8=0的两个实数根,且
| x | 2 1 |
| x | 2 2 |
分析:(1)、(2)根据根与系数的关系:x1+x2=-
,x1•x2=
,来解题.
(3)首先根据根的判别式求得m的取值范围,然后由根与系数的关系来求m的值.
| b |
| a |
| c |
| a |
(3)首先根据根的判别式求得m的取值范围,然后由根与系数的关系来求m的值.
解答:解:(1)∵x1、x2是方程x2-4x+
=0的两个实数根,
∴x1+x2=-
=4,x1•x2=
=
;
故答案是:4,
;
(2)∵x1、x2是方程2x2+6x-3=0的两个实数根,
∴x1+x2=
=3,x1•x2=
=-
,
∴
+
=
=
=-2,
+
=(x1+x2)2-2x1•x2=32-2×(-
)=12.
故答案是:-2,12;
(3)∵关于x的方程x2-(m-3)x+m+8=0有两个实数根,
∴△=(m-3)2-4(m+8)≥0,即m≥5+4
,或m≤5-4
∵x1、x2是关于x的方程x2-(m-3)x+m+8=0的两个实数根,
∴x1+x2=m-3,x1•x2=m+8,
∴
+
=(x1+x2)2-2x1•x2=13,即(m-3)2-2(m+8)=13,
解得,m=-2或m=10.
即m的值是-2或10.
| 5 |
∴x1+x2=-
| -4 |
| 1 |
| ||
| 1 |
| 5 |
故答案是:4,
| 5 |
(2)∵x1、x2是方程2x2+6x-3=0的两个实数根,
∴x1+x2=
| 6 |
| 2 |
| -3 |
| 2 |
| 3 |
| 2 |
∴
| 1 |
| x1 |
| 1 |
| x2 |
| x1+x2 |
| x1•x2 |
| 3 | ||
-
|
| x | 2 1 |
| x | 2 2 |
| 3 |
| 2 |
故答案是:-2,12;
(3)∵关于x的方程x2-(m-3)x+m+8=0有两个实数根,
∴△=(m-3)2-4(m+8)≥0,即m≥5+4
| 3 |
| 3 |
∵x1、x2是关于x的方程x2-(m-3)x+m+8=0的两个实数根,
∴x1+x2=m-3,x1•x2=m+8,
∴
| x | 2 1 |
| x | 2 2 |
解得,m=-2或m=10.
即m的值是-2或10.
点评:此题主要考查了根与系数的关系,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.

练习册系列答案
相关题目
 ,x1x2=
,x1x2= .∵
.∵
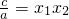 ,∴
,∴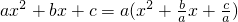 =a[x2-(x1+x2)x+x1x2]=a(x-x1)(x-x2).于是,二次三项式就可以分解因式ax2+bx+c=a(x-x1)(x-x2).
=a[x2-(x1+x2)x+x1x2]=a(x-x1)(x-x2).于是,二次三项式就可以分解因式ax2+bx+c=a(x-x1)(x-x2). ,x1x2=
,x1x2= .
.
 ,
, =a[x2﹣(x1+x2)x+x1x2]=a(x﹣x1)(x﹣x2).
=a[x2﹣(x1+x2)x+x1x2]=a(x﹣x1)(x﹣x2). ,x1x2=
,x1x2= .∵
.∵
 ,∴
,∴ =a[x2-(x1+x2)x+x1x2]=a(x-x1)(x-x2).于是,二次三项式就可以分解因式ax2+bx+c=a(x-x1)(x-x2).
=a[x2-(x1+x2)x+x1x2]=a(x-x1)(x-x2).于是,二次三项式就可以分解因式ax2+bx+c=a(x-x1)(x-x2).