题目内容
26、游戏机的“方块”中共有下面7种图形.每种“方块”都由4个l×l的小方格组成.现用这7种图形拼成一个7×4的长方形(可以重复使用某些图形).
问:最多可以用这7种图形中的几种图形?
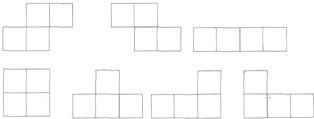
问:最多可以用这7种图形中的几种图形?

分析:为了形象化地说明问题,对7×4的长方形的28个小方格黑白相间染色,除“品字型”必占3个黑格1个白格或3个白格1个黑格,其余6个方格各占2个黑格2个白格.
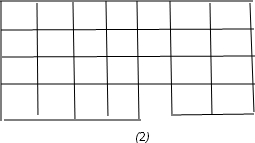
解答:解:用其中的六种不同的图形方块可以拼成7×4的长方形,如图①仅出示一种.
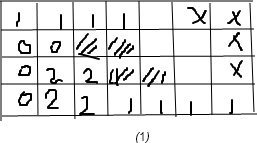
下面证明不能7种图形方块各有一次,将7×4的长方形的28个小方格黑白相间染色.
则如图②所示,黑白格各14个,若7×4的长方形能用7个不同的方块拼成,
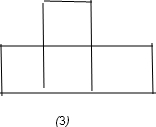
则每个方块用到一次且只用一次,其中“品字形”如图③必占3个黑格,1个白格或3个白格1个黑格,
其余6个方块各占2个黑格2个白格,7个不同的方块占据的黑格总数,白格总数都是奇数个,不会等于14.
矛盾,因此不存在7种图形方块每个各用一次,拼成7×4的长方形的方法.
所以,要拼成7×4的长方形,最多可以用这7种图形方块中的6种.
下面证明不能7种图形方块各有一次,将7×4的长方形的28个小方格黑白相间染色.
则如图②所示,黑白格各14个,若7×4的长方形能用7个不同的方块拼成,
则每个方块用到一次且只用一次,其中“品字形”如图③必占3个黑格,1个白格或3个白格1个黑格,
其余6个方块各占2个黑格2个白格,7个不同的方块占据的黑格总数,白格总数都是奇数个,不会等于14.
矛盾,因此不存在7种图形方块每个各用一次,拼成7×4的长方形的方法.
所以,要拼成7×4的长方形,最多可以用这7种图形方块中的6种.



点评:本题考查在一定的规则下,进行某种操作或变换,问是否(或证明)能够达到一个预期的目的,这就是所谓操作变换问题,此类问题变化多样,解法灵活,解题的关键是在操作变换中,挖掘不变量,不变性.

练习册系列答案
相关题目
 24、在排成每行七天的日历表中取下一个3×3方块(如图).若所有日期数之和为189,则n的值为( )
24、在排成每行七天的日历表中取下一个3×3方块(如图).若所有日期数之和为189,则n的值为( )

