题目内容
三角形内角平分线的交点为三角形的内心．如图，D是△ABC的内心，E是△ABD的内心，F是△BDE的内心．若∠BFE的度数为整数，则∠BFE至少是________°．
113
分析：首先由三角形内角的性质，求得，∠ADB=90°+
，∠BED=90°+
，∠BFE=90°+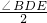
，又由∠BFE的度数为整数，即可求得∠BEF的最小值．
解答：∵D是△ABC的内心，E是△ABD的内心，F是△DBE的内心，
∴∠BDE=
∠ADB，∠ADB=90°+，∠BED=90°+，∠BFE=90°+，
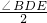∴∠BFE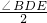=90°+=90°+
∠ADB=90°+（90°+∠C）=112.5°+
∠C，
∵∠BFE的度数为整数，
∴当∠C=4°时，∠BFE=113°最小，
故答案为113°．
点评：此题考查了三角形内心的性质．注意三角形的内心即是三角形角平分线的交点．
分析：首先由三角形内角的性质，求得，∠ADB=90°+
，∠BED=90°+，∠BFE=90°+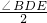，又由∠BFE的度数为整数，即可求得∠BEF的最小值．解答：∵D是△ABC的内心，E是△ABD的内心，F是△DBE的内心，
∴∠BDE=
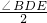∠ADB，∠ADB=90°+，∠BED=90°+，∠BFE=90°+，∴∠BFE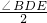=90°+
=90°+∠ADB=90°+（90°+∠C）=112.5°+∠C，∵∠BFE的度数为整数，
∴当∠C=4°时，∠BFE=113°最小，
故答案为113°．
点评：此题考查了三角形内心的性质．注意三角形的内心即是三角形角平分线的交点．
练习册系列答案
智能训练练测考系列答案
相关题目
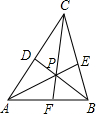通过学习我们已经知道三角形的三条内角平分线是交于一点的．如图，P是△ABC的内角平分线的交点，已知P点到AB边的距离为1，△ABC的周长为10，则△ABC的面积为
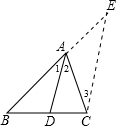E∥AD，交BA的延长线于E，从而得到BD、DC、AB的第四比例项AE，这样，证明
[]
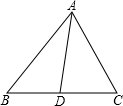24、先阅读下面的材料，然后解答问题：
