题目内容
 如图,已知一艘轮船以20海里/时的速度由西向东航行,途中接到台风警报,台风中心正以40海里/时的速度由南向北移动,距台风中心20
如图,已知一艘轮船以20海里/时的速度由西向东航行,途中接到台风警报,台风中心正以40海里/时的速度由南向北移动,距台风中心20| 10 |
分析:设途中会遇到台风,且最初遇到台风的时间为t小时,此时轮船位于C处,台风中心移到E处,连接CE,根据勾股定理列方程求解即可.
解答:解:设途中会遇到台风,且最初遇到的时间为th,此时轮船位于C处,台风中心移到E处,连接CE,
则AC=20t,
AE=AB-BE=100-40t,
AC2+AE2=EC2.
∴(20t)2+(100-40t)2=(20
)2
400t2+10000-8000t+1600t2=4000
t2-4t+3=0
(t-1)(t-3)=0,
解得t1=1,t2=3(不合题意舍去).
答:最初遇到的时间为1h.
则AC=20t,
AE=AB-BE=100-40t,
AC2+AE2=EC2.
∴(20t)2+(100-40t)2=(20
| 10 |
400t2+10000-8000t+1600t2=4000
t2-4t+3=0
(t-1)(t-3)=0,
解得t1=1,t2=3(不合题意舍去).
答:最初遇到的时间为1h.
点评:此题用到了路程公式和勾股定理.找到关键描述语,找到等量关系准确的列出方程是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
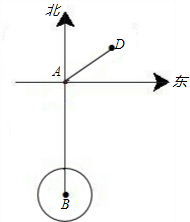 中新网2010年8月23日电.中央气象台消息,今日8时,南海热带低压加强为今年第5号热带风暴“蒲公英”,逐渐向海南岛南部近海靠近.已知,如图,一艘轮船以20海里/时的速度由西向东航行,在途中接到台风警报,台风中心正以40海里/时的速度由南向北移动,距台风中心
中新网2010年8月23日电.中央气象台消息,今日8时,南海热带低压加强为今年第5号热带风暴“蒲公英”,逐渐向海南岛南部近海靠近.已知,如图,一艘轮船以20海里/时的速度由西向东航行,在途中接到台风警报,台风中心正以40海里/时的速度由南向北移动,距台风中心 如图,已知灯塔M方圆一定范围内有镭射辅助信号,一艘轮船在海上从南向北方向以一定的速度匀速航行,轮船在A处测得灯塔M在北偏东30°方向,行驶1小时后到达B处,此时刚好进入灯塔M的镭射信号区,测得灯塔M在北偏东45°方向,则轮船通过灯塔M的镭射信号区的时间为( )
如图,已知灯塔M方圆一定范围内有镭射辅助信号,一艘轮船在海上从南向北方向以一定的速度匀速航行,轮船在A处测得灯塔M在北偏东30°方向,行驶1小时后到达B处,此时刚好进入灯塔M的镭射信号区,测得灯塔M在北偏东45°方向,则轮船通过灯塔M的镭射信号区的时间为( ) 海里的圆形区域(包括边界)都属台风区.当轮船到A处时,测得台风中心移到位于点A正南方向B处,且AB=100海里,若这艘轮船自A处按原速度继续航行,在途中会不会遇到台风?若会,试求轮船最初遇到台风的时间;若不会,请说明理由.
海里的圆形区域(包括边界)都属台风区.当轮船到A处时,测得台风中心移到位于点A正南方向B处,且AB=100海里,若这艘轮船自A处按原速度继续航行,在途中会不会遇到台风?若会,试求轮船最初遇到台风的时间;若不会,请说明理由.
 海里的圆形区域(包括边界)都属台风区.当轮船到A处时,测得台风中心移到位于点A正南方向B处,且AB=100海里,若这艘轮船自A处按原速度继续航行,在途中会不会遇到台风?若会,试求轮船最初遇到台风的时间;若不会,请说明理由.
海里的圆形区域(包括边界)都属台风区.当轮船到A处时,测得台风中心移到位于点A正南方向B处,且AB=100海里,若这艘轮船自A处按原速度继续航行,在途中会不会遇到台风?若会,试求轮船最初遇到台风的时间;若不会,请说明理由.