题目内容
已知方程x2+kx+1=0的一个根是 ,则k=________,另一根为________.
,则k=________,另一根为________.
-2
 -1
-1
分析:由1+ 为方程的解,故将1+
为方程的解,故将1+ 代入方程得到关于k的方程,求出方程的解得到k的值,然后再由根与系数的关系得到两根之积为1,由一个解为1+
代入方程得到关于k的方程,求出方程的解得到k的值,然后再由根与系数的关系得到两根之积为1,由一个解为1+ ,即可求出方程的另一个解.
,即可求出方程的另一个解.
解答:∵x2+kx+1=0的一个根是1+ ,
,
∴将x=1+ 代入方程得:(1+
代入方程得:(1+ )2+(1+
)2+(1+ )k+1=0,
)k+1=0,
解得:k=-2 ,
,
又两根之积为1,
∴方程的另一个解为: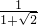 =
= -1.
-1.
故答案为:-2 ;
; -1.
-1.
点评:此题考查了一元二次方程的解,以及根与系数的关系,方程的解为能使方程左右两边相等的未知数的值,一元二次方程ax2+bx+c=0(a≠0),当b2-4ac≥0时,方程有解,设方程的解分别为x1,x2,则有x1+x2=- ,x1x2=
,x1x2= .
.

 -1
-1分析:由1+
 为方程的解,故将1+
为方程的解,故将1+ 代入方程得到关于k的方程,求出方程的解得到k的值,然后再由根与系数的关系得到两根之积为1,由一个解为1+
代入方程得到关于k的方程,求出方程的解得到k的值,然后再由根与系数的关系得到两根之积为1,由一个解为1+ ,即可求出方程的另一个解.
,即可求出方程的另一个解.解答:∵x2+kx+1=0的一个根是1+
 ,
,∴将x=1+
 代入方程得:(1+
代入方程得:(1+ )2+(1+
)2+(1+ )k+1=0,
)k+1=0,解得:k=-2
 ,
,又两根之积为1,
∴方程的另一个解为:
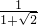 =
= -1.
-1.故答案为:-2
 ;
; -1.
-1.点评:此题考查了一元二次方程的解,以及根与系数的关系,方程的解为能使方程左右两边相等的未知数的值,一元二次方程ax2+bx+c=0(a≠0),当b2-4ac≥0时,方程有解,设方程的解分别为x1,x2,则有x1+x2=-
 ,x1x2=
,x1x2= .
. 
练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目