题目内容
 如图所示,在直角梯形ABCD中,AB⊥BC,AD=1,BC=3,CD=4,EF为梯形的中位线,DH为梯形的高且交EF于点G,下列结论:①G为EF的中点;②△EHF为等边三角形;③四边形EHCF为菱形;④S△BEH=S△CFH,其中正确的结论有
如图所示,在直角梯形ABCD中,AB⊥BC,AD=1,BC=3,CD=4,EF为梯形的中位线,DH为梯形的高且交EF于点G,下列结论:①G为EF的中点;②△EHF为等边三角形;③四边形EHCF为菱形;④S△BEH=S△CFH,其中正确的结论有
- A.1个
- B.2个
- C.3个
- D.4个
C
分析:根据梯形的中位线定理求相关线段的长度后求解.
解答:①∵EF为梯形的中位线,DH为梯形的高,EG=AD=BH=1,GF= HC=
HC= (BC-BH)=
(BC-BH)= ×2=1.
×2=1.
∴G为EF的中点,正确;
②∵EF∥BC,DH为BC边上的高,
∴DH⊥BC,
∴DH⊥EF.又∵EG=GF,
∴EH=HF.
∵EF为梯形的中位线,
∴DG=GH,△EHG≌△FDG.
∴DF=EH=HF=2,EF=2.故△EHF为等边三角形.正确;
③有以上结论可知EH=HC=CF=EF=2.
∴四边形EHCF为菱形,正确;
④∵两个三角形同高,但底不相同.
∴S△BEH=S△CFH,不正确.
故选C.
点评:本题比较复杂,信息量较大,需要同学们熟知梯形及三角形中位线定理.
分析:根据梯形的中位线定理求相关线段的长度后求解.
解答:①∵EF为梯形的中位线,DH为梯形的高,EG=AD=BH=1,GF=
 HC=
HC= (BC-BH)=
(BC-BH)= ×2=1.
×2=1.∴G为EF的中点,正确;
②∵EF∥BC,DH为BC边上的高,
∴DH⊥BC,
∴DH⊥EF.又∵EG=GF,
∴EH=HF.
∵EF为梯形的中位线,
∴DG=GH,△EHG≌△FDG.
∴DF=EH=HF=2,EF=2.故△EHF为等边三角形.正确;
③有以上结论可知EH=HC=CF=EF=2.
∴四边形EHCF为菱形,正确;
④∵两个三角形同高,但底不相同.
∴S△BEH=S△CFH,不正确.
故选C.
点评:本题比较复杂,信息量较大,需要同学们熟知梯形及三角形中位线定理.

练习册系列答案
相关题目
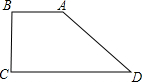 如图所示,在直角梯形ABCD中,AB∥CD,∠B=∠C=90°,AD=20,BC=10,则∠A和∠D分别是( )
如图所示,在直角梯形ABCD中,AB∥CD,∠B=∠C=90°,AD=20,BC=10,则∠A和∠D分别是( )| A、30°,150° | B、45°,135° | C、120°,60° | D、150°,30° |
 27、如图所示,在直角梯形ABCD中,AD∥BC,AD=24cm,AB=8cm,BC=26cm,动点P从A点开始沿AD边向D以1cm/s的速度运动,动点Q从C点开始沿CB边向B以3cm/s的速度运动.P,Q分别从A,C同时出发,当其中一点到端点时,另一点也随之停止运动,设运动时间为t(s),t分别为何值时,四边形PQCD是平行四边形?等腰梯形?
27、如图所示,在直角梯形ABCD中,AD∥BC,AD=24cm,AB=8cm,BC=26cm,动点P从A点开始沿AD边向D以1cm/s的速度运动,动点Q从C点开始沿CB边向B以3cm/s的速度运动.P,Q分别从A,C同时出发,当其中一点到端点时,另一点也随之停止运动,设运动时间为t(s),t分别为何值时,四边形PQCD是平行四边形?等腰梯形?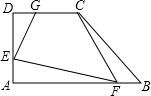 如图所示,在直角梯形ABCD中,∠A=∠D=90°,截取AE=BF=DG=x.已知AB=6,CD=3,AD=4.求四边形CGEF的面积S关于x的函数表达式和x的取值范围.
如图所示,在直角梯形ABCD中,∠A=∠D=90°,截取AE=BF=DG=x.已知AB=6,CD=3,AD=4.求四边形CGEF的面积S关于x的函数表达式和x的取值范围.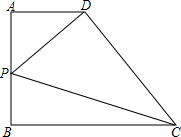 如图所示,在直角梯形ABCD中,AB=2,P是边AB的中点,∠PDC=90°,问梯形ABCD面积的最小值是多少?
如图所示,在直角梯形ABCD中,AB=2,P是边AB的中点,∠PDC=90°,问梯形ABCD面积的最小值是多少? (2013•山西模拟)如图所示,在直角梯形ABCD中,AB∥CD,点E为AB的中点,点F为BC的中点,AB=4,EF=2,∠B=60°,则AD的长为
(2013•山西模拟)如图所示,在直角梯形ABCD中,AB∥CD,点E为AB的中点,点F为BC的中点,AB=4,EF=2,∠B=60°,则AD的长为