��Ŀ����
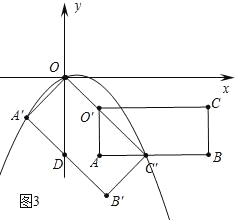
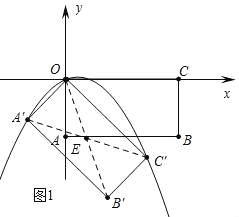
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����OABC�Ķ���OΪ����ԭ�㣬����A��C������ֱ�Ϊ��0����![]() ������2
������2![]() ��0����������OABC�Ƶ�O˳ʱ����ת45��õ�����OA��B��C�䣬��A��B����y�ύ�ڵ�D����������ԭ���������y=ax2+bxͬʱ������A�䡢C�䣮
��0����������OABC�Ƶ�O˳ʱ����ת45��õ�����OA��B��C�䣬��A��B����y�ύ�ڵ�D����������ԭ���������y=ax2+bxͬʱ������A�䡢C�䣮
��1��������������Ӧ�ĺ�������ʽ��
��2��д����B������ꣻ
��3����P�DZ�OC����һ�㣬����P��PQ��OC�䣬��������λ��y���Ҳಿ���ڵ�Q������OQ��DQ������ODQ�����ΪS����ֱ��PQ������OA��B��C��������Ϊ1��3��������ʱ����S��ֵ��
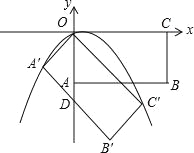
��4�����־���OA��B��C�䲻����������OABC������CO������ÿ��1����λ���ȵ��ٶ�ƽ�ƣ���ƽ��ʱ��Ϊt�루t��0����������OABC�����OA��B��C���ص�����ͼ��Ϊ��Գƶ����ʱ��ֱ��д��t��ȡֵ��Χ��
���𰸡���1�������ߵĽ���ʽΪy=��![]() x2+
x2+![]() x��
x��
��2��B�䣨1����3����
��3��S��ODQ��=![]() ��2��
��2��![]() =
=![]() ��
��
��4��0��t![]() ��2��t=
��2��t=![]() ��2
��2![]() ��1��t��2
��1��t��2![]() ʱ������OABC�����OA��B��C���ص�����ͼ��Ϊ��Գƶ���Σ�
ʱ������OABC�����OA��B��C���ص�����ͼ��Ϊ��Գƶ���Σ�
��������
�����������1�����A��C�������꣬��A��C�����������y=ax2+bx�ⷽ���鼴�ɣ�
��2����ͼ1�У�����A��C�䣬OB�佻�ڵ�E�������E���꣬�����е����깫ʽ���ɽ�����⣮
��3�����������ٵ�OP��PC��=1��3ʱ��P��![]() ����
����![]() �������ֱ��PQ�Ľ���ʽ�����÷����������Q���꼴�ɣ��ڵ�OP�䣺P��C��=3��1ʱ��P�䣨
�������ֱ��PQ�Ľ���ʽ�����÷����������Q���꼴�ɣ��ڵ�OP�䣺P��C��=3��1ʱ��P�䣨![]() ����
����![]() �����������ƣ�
�����������ƣ�
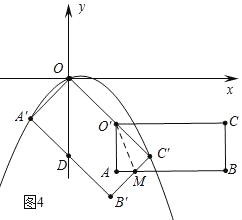
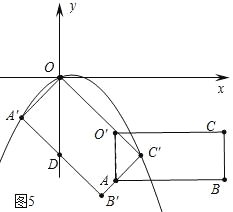
��4���ֱ��������ͼ3�У���AB������C��ʱ������ͼ4�У���O��C��=O��A=![]() ʱ������ͼ5�У�����A��ֱ��B��C����ʱ��ʱ��t���۲�ͼ�ɽ�����⣮
ʱ������ͼ5�У�����A��ֱ��B��C����ʱ��ʱ��t���۲�ͼ�ɽ�����⣮
�����������1����ͼ1�У�
������A�䣨��1����1����C�䣨2����2������A�䣨��1����1����C�䣨2����2������y=ax2+bx��![]() ��
��
���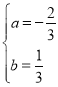 ��
��
�������ߵĽ���ʽΪy=��![]() x2+
x2+![]() x��
x��
��2����ͼ1�У�����A��C�䣬OB�佻�ڵ�E�����ı���OA��B��C���Ǿ��Σ�
��A��E=EC�䣬OE=EB�䣬��A�䣨��1����1����C�䣨2����2������E��![]() ����
����![]() ������B�䣨1����3����
������B�䣨1����3����
��3����ͼ2�У���ֱ��PQ������OA��B��C��������Ϊ1��3�������֣�
��OP��PC��=1��3��OP�䣺P��C��=3��1��
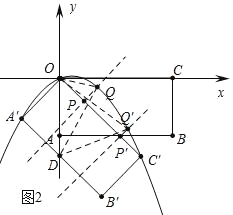
�ٵ�OP��PC��=1��3ʱ��P��![]() ����
����![]() ����ֱ��PQ�Ľ���ʽΪy=x��1��
����ֱ��PQ�Ľ���ʽΪy=x��1��
��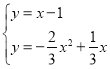 �����
�����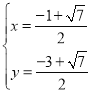 ��
��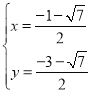 ������Q�ڵ������ޣ�
������Q�ڵ������ޣ�
��Q��![]() ��
��![]() ������D��0����2������S��ODQ=
������D��0����2������S��ODQ=![]() ��2��
��2��![]() =
=![]() ��
��
�ڵ�OP�䣺P��C��=3��1ʱ��P�䣨![]() ����
����![]() ������ֱ��P��Q��Ľ���ʽΪy=x��3��
������ֱ��P��Q��Ľ���ʽΪy=x��3��
��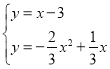 ���
���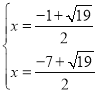 ��
��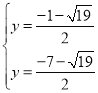 ��
��
��Q�䣨![]() ��
��![]() ������S��ODQ��=
������S��ODQ��=![]() ��2��
��2��![]() =
=![]() ��
��
��4����ͼ3�У���AB������C��ʱ��t=2![]() ��2��
��2��
��ͼ4�У���O��C��=O��A=![]() ʱ��AB��B��C�佻�ڵ�M������O��M������O��MA�ա�O��MC�䣬
ʱ��AB��B��C�佻�ڵ�M������O��M������O��MA�ա�O��MC�䣬
��ʱt=OO��=2![]() ��
��![]() =
=![]() ��
��
��ͼ5�У�����A��ֱ��B��C��ʱ�ϣ�t=OO��=2![]() ��1��
��1��
�����������۲�ͼ�ο�֪0��t![]() ��2��t=
��2��t=![]() ��2
��2![]() ��1��t��2
��1��t��2![]() ʱ������OABC�����OA��B��C���ص�����ͼ��Ϊ��Գƶ���Σ�
ʱ������OABC�����OA��B��C���ص�����ͼ��Ϊ��Գƶ���Σ�