Question

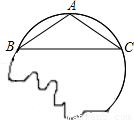
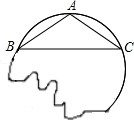小明家位于六朝古都西安，一个星期天的早晨，小明吃过早饭，像往常一样来到菜地，帮助妈妈锄草，“铛”的一声，引起小明的注意，好奇的小明发现草丛下面的土里，有一个圆形的破损的古镜，爱动脑筋的小明想知道这个古镜的半径大小，他在古镜上随意找到了三个点A、B、C．若构成的△ABC恰好是等腰三角形，底边BC=8cm，腰AB=5cm，你能帮忙计算镜子的半径吗？

Answer 1

分析：首先找到圆心，连接AO，OB，利用垂径定理和勾股定理可求出圆片的半径R．

解答：解：连接AO，OB，
∵△ABC恰好是等腰三角形，
∴AB=AC，∴

AB

=

AC

，
∴AO⊥BC，
∵BC=8cm，
∴BD=4cm，
∵AB=5cm，
∴AD=

52-42

=3（cm），
设圆片的半径为R，在Rt△BOD中，OD=（R-3）cm，
∴R²=5²+（R-3）²，
解得：R=8.5（cm），
答：圆片的半径R为8.5cm．

点评：本题主要考查了垂径定理的推论，我们可以把垂径定理的题设和结论这样叙述：一条直线①过圆心，②垂直于弦，③平分弦，④平分优弧，⑤平分劣弧．在应用垂径定理解题时，只要具备上述5条中任意2条，则其他3条成立．