题目内容
 如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫格点,请在给定的网格中按要求画图:
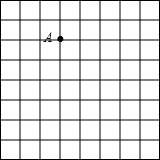
如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫格点,请在给定的网格中按要求画图:(1)从点A出发在图中画一条线段AB,使得AB=
| 20 |
(2)画出一个以(1)中的AB为斜边的等腰直角三角形,使三角形的三个顶点都在格点上,并根据所画图形求出等腰直角三角形的腰长.
分析:(1)根据20=22+42,则B点与A点相差横2竖4即可,可画出AB线段如图;
(2)AB长为
,根据题意,AB为等腰直角三角形的斜边,则腰长为
×
=
.
(2)AB长为
| 20 |
| 20 |
| ||
| 2 |
| 10 |
解答:解:
(1)图示线段AB长为
=
;
(2)图中A、B、C均在方格的顶点上,
且AC2=BC2=12+32,
AB2=22+42
∴AC2+BC2=AB2,
∴图中等腰直角△满足题意.

(1)图示线段AB长为
| 22+42 |
| 20 |
(2)图中A、B、C均在方格的顶点上,
且AC2=BC2=12+32,
AB2=22+42
∴AC2+BC2=AB2,
∴图中等腰直角△满足题意.
点评:本题考查了勾股定理的灵活运用,本题中找到合适的线段AB使得B落在方格顶点上是解题的关键

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


 (1)先化简,再求值:x(x-2)-(x+1)(x-1),其中x=10.
(1)先化简,再求值:x(x-2)-(x+1)(x-1),其中x=10.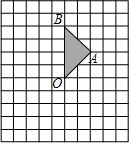 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABO的三个顶点A,B,O都在格点上.
如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABO的三个顶点A,B,O都在格点上.