题目内容
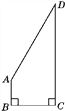
【题目】某校一块空地被荒废，如图，为了绿化环境，学校打算利用这块空地种植花草，已知AB⊥BC，CD⊥BC，AB＝
CD＝
m，BC＝3
m，试求这块空地的面积．
【答案】
(m2)
【解析】试题分析：过点A作AE⊥DC于点E，根据AB=
CD=
m即可求出DE、CD的值，进而利用勾股定理求出AD的值；根据矩形以及直角三角形的面积公式以及周长的计算方法，即可解决.
试题解析：过点A作AE⊥DC于点E，如图所示.
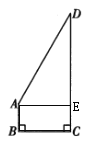
∵AB=
CD=
m，AE⊥CD，
∴CD=4
m ，DE=3
m，
∵AB⊥BC，CD⊥BC ，AE⊥CD， BC=3
m，
∴四边形ABCE为矩形，
∴AE=BC=3
m，
∵AE=3
m ，DE=3
m，
∴AD=6
m，
∵四边形ABCE为矩形，△AED为直角三角形，
∴空地的周长=AB+BC+CD+AD=9
+5
（m）
空地的面积=AB·BC+
AE·DE=15
(m3).
练习册系列答案
阅读快车系列答案
相关题目
