题目内容
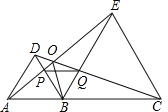
【题目】如图,已知点A、B、C在同一直线上,△ABD和△BCE都是等边三角形.则在下列结论中:①AP=DQ,②EP=EC,③PQ=PB,④∠AOB=∠BOC=∠COE.正确的结论是 (填写序号).

【答案】①③④.
【解析】
试题分析:易证△ABE≌△DBC,则有∠BAE=∠BDC,从而可证到△ABP≌△DBQ,则有AP=DQ,BP=BQ,由∠PBQ=60°可得△BPQ是等边三角形,则有PQ=PB.∠BPQ=60°,从而可得∠EPB>∠EBP,即可得到EB>EP,即EC>EP,由△ABE≌△DBC可得S△ABE=S△DBC,AE=DC,从而可得点B到AE、DC的距离相等,因而点B在∠AOC的角平分线上,即可得到∠AOB=∠BOC=∠COE=60°.
解:∵△ABD和△BCE都是等边三角形,
∴BD=BA=AD,BE=BC=EC,∠ABD=∠CBE=60°,
∵点A、B、C在同一直线上,
∴∠DBE=180°﹣60°﹣60°=60°,
∴∠ABE=∠DBC=120°.
在△ABE和△DBC中,
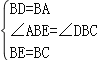 ,
,
∴△ABE≌△DBC,
∴∠BAE=∠BDC.
在△ABP和△DBQ中,
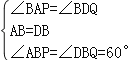 ,
,
∴△ABP≌△DBQ,
∴AP=DQ,BP=BQ.
∴①正确.
∵∠PBQ=60°,
∴△BPQ是等边三角形,
∴PQ=PB.∠BPQ=60°.
∴③正确.
∵∠EPB>∠BPQ,∠BPQ=∠EBP=60°,
∴∠EPB>∠EBP,
∴EB>EP,
∴EC>EP,
∴②不正确.
∵∠DPA=∠PDO+∠DOP,∠DPA=∠PAB+∠ABP,∠PDO=∠PAB,
∴∠DOP=∠ABP=60°,
∴∠COE=60°,∠AOC=120°.
∵△ABE≌△DBC,
∴S△ABE=S△DBC,AE=DC,
∴点B到AE、DC的距离相等,
∴点B在∠AOC的角平分线上,
∴∠AOB=∠BOC=![]() ∠AOC=60°,
∠AOC=60°,
∴∠AOB=∠BOC=∠COE=60°.
∴④正确.
故答案为①③④.