题目内容
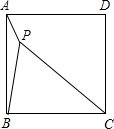 如图,P为正方形ABCD内一点,若PA=a,PB=2a,PC=3a(a>0).
如图,P为正方形ABCD内一点,若PA=a,PB=2a,PC=3a(a>0).
(1)求∠APB的度数;
(2)求正方形ABCD的面积.
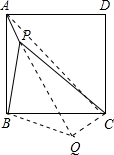 解:(1)将△ABP绕点B顺时针方向旋转90°得△CBQ,如图,
解:(1)将△ABP绕点B顺时针方向旋转90°得△CBQ,如图,则△ABP≌△CBQ且PB⊥QB,
于是PB=QB=2a,PQ=2
 a,
a,在△PQC中,
∵PC2=9a2,PQ2+QC2=9a2,
∴PC2=PQ2+QC2.
∴∠PQC=90°,
∵△PBQ是等腰直角三角形,
∴∠BPQ=∠BQP=45°,故∠APB=∠CQB=90°+45°=135°;
(2)∵∠APQ=∠APB+∠BPQ=135°+45°=180°,
∴三点A、P、Q在同一直线上,
在Rt△AQC中,AC2=AQ2+QC2=(a+2
 a)2+a2=(10+4
a)2+a2=(10+4 )a2,
)a2,∴正方形ABCD的面积
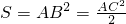 =(5+2
=(5+2 )a2.
)a2.分析:(1)已知PA=a,PB=2a,PC=3a,并不在同一个三角形中,因为AB=BC,可将△ABP绕点B顺时针方向旋转90°得△CBQ,连接PQ,构成两个特殊三角形,可求∠APB的度数;
(2)用(1)的结论,证明∠APQ=180°,得出△AQC是直角三角形,根据AQ,QC的长及勾股定理求AC,从而可求正方形ABCD的面积.
点评:利用旋转的方法,把图形转移位置,使条件相对集中,可为证明和计算提供条件.

练习册系列答案
相关题目
 17、如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点,△DAE旋转后能与△DCF重合.
17、如图,E为正方形ABCD的边AB上一点(不含A、B点),F为BC边的延长线上一点,△DAE旋转后能与△DCF重合. OM方向以
OM方向以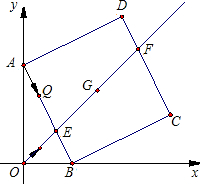 向以
向以
 (2009•梅州一模)如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙0与BC相切于点M,与AB、AD分别相交于点E、F.
(2009•梅州一模)如图,O为正方形ABCD对角线AC上一点,以O为圆心,OA长为半径的⊙0与BC相切于点M,与AB、AD分别相交于点E、F.