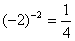题目内容
已知：a，b，c为△ABC的三边长，且2a2＋2b2＋2c2＝2ab＋2ac＋2bc，试判断
△ABC的形状，并证明你的结论．
解：△ABC是等边三角形．证明如下：
因为2a2＋2b2＋2c2＝2ab＋2ac＋2bc，所以2a2＋2b2＋2c2－2ab－2ac－2bc＝0，
a2－2ab＋b2＋a2－2ac＋c2＋b2－2bc＋c2＝0，
(a－b)2＋(a－c)2＋(b－c)2＝0，
所以(a－b)2＝0，(a－c
)2＝
0，(b－c)2＝0，得a＝b且a＝c且b＝c，即a＝b＝c，所以△ABC是等边三角形．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
（1）作线段AB的中垂线E
F（5分）（2）作∠AOB的角平分线OC（5分） 
一个车站P，使得P向A，B两个地方的距离和最小，
请在图中画出P的位置。 （5分）
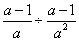的结果是( )．
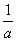B．a C．a－1 D．
＝__________.
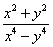=2
其中正确的有( )
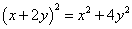
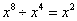D．