题目内容
 如图,以△ABC的边AB为直径的⊙O交AC于点D,弦DE∥AB,∠C=∠BAF
如图,以△ABC的边AB为直径的⊙O交AC于点D,弦DE∥AB,∠C=∠BAF
(1)求证:BC为⊙O的切线;
(2)若⊙O的半径为5,AD= ,求DE的长.
,求DE的长.
 (1)证明:连BD,则∠CDB=90°
(1)证明:连BD,则∠CDB=90°∠C=∠BAF=∠BDE
∵DE∥AB
∴∠ABD=∠BDE=∠C
∴∠ABC=∠ABD+∠DBC=∠C+∠DBC=90°
∴BC为⊙O的切线;
(2)解:过D作DM⊥AB,
∵AB=10,AD=
 ,
,∴在Rt△ADB中,DB=
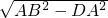 =
=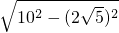 =4
=4 ,
,又∵S△ADB=
 AD•DB=
AD•DB= AB•DM,
AB•DM,∴DM=4,
在Rt△ADM中,AM=
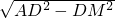 =
=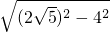 =2
=2 ∴DE=AB-2AM=10-2×2=6.
分析:(1)连接BD.欲证BC为⊙O的切线,只需证明∠ABC=90°即可;
(2)过D作DM⊥AB,在Rt△ADB中利用勾股定理即可求得DB的长,然后根据三角形的面积公式即可求得DM的长,即DE的弦心距,则DE=AB-2AM,据此即可求解.
点评:本题考查切线的判定以及勾股定理,已知所证的直线经过圆上的点,证切线常用的方法是转化成证垂直.

练习册系列答案
相关题目
 26、如图,以△ABC的边AB、AC为边的等边三角ABD和等边三角形ACE,四边形ADFE是平行四边形.
26、如图,以△ABC的边AB、AC为边的等边三角ABD和等边三角形ACE,四边形ADFE是平行四边形.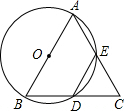 如图,以△ABC的边AB为直径作⊙O,交BC于D点,交AC于E点,BD=DE
如图,以△ABC的边AB为直径作⊙O,交BC于D点,交AC于E点,BD=DE
 (2011•峨眉山市二模)如图,以△ABC的边AB为直径作⊙O,BC与⊙O交于D,D是BC的中点,过D作DE⊥AC,交AC于点E.
(2011•峨眉山市二模)如图,以△ABC的边AB为直径作⊙O,BC与⊙O交于D,D是BC的中点,过D作DE⊥AC,交AC于点E. (2010•黔东南州)如图,以△ABC的边BC为直径作⊙O分别交AB,AC于点F.点E,AD⊥BC于D,AD交于⊙O于M,交BE于H.
(2010•黔东南州)如图,以△ABC的边BC为直径作⊙O分别交AB,AC于点F.点E,AD⊥BC于D,AD交于⊙O于M,交BE于H. 如图,以△ABC的边AB为直径的⊙O交AC于点D,弦DE∥AB,∠C=∠BAF
如图,以△ABC的边AB为直径的⊙O交AC于点D,弦DE∥AB,∠C=∠BAF